Uniswap v3 introduced restricted ranges to address automated market maker capital efficiency. An alternative way to economize capital would give liquidity providers leverage. I will refer to this as a leveraged v2 contract or LAMM (Leveraged Automated Market Maker).
I made a prototype that works on Rinkeby here (you can see the contract code here).
Adding leverage to an AMM has several benefits in addition to capital efficiency. For example, given the ability to extend leverage to LPs, extending leverage to traders is straightforward. This means a leveraged swap contract can allow traders to short and leverage long, previously only available in perpetual swap (‘perp’) markets. This perp market would have the added benefit of not requiring an oracle because the price is set by arbitrage, in that an underpriced token can be bought on the LAMM and then sold on another exchange at a higher price. This avoids the ridiculous funding rate premium mechanism, which is simply a conspiracy by insiders to milk extra revenue out of users (to see why it does and cannot ‘arbitrage’ the perp price see here).
There are several other significant advantages to using a leveraged AMM compared to restricted ranges. For example, with leverage account insolvency is possible, there needs to be a reserve or insurance fund within the contract to prevent contract insolvency. In corporate financial theory, equity is often thought of as the residual tranche, the part of the capital structure that takes the first loss and that part that takes any extra revenue. Equity holders have rights and responsibilities, so they are correctly incented to make the contract work well; equity receives revenue for an essential continual service. In contrast, adding a fee to Uniswap going to their equity holders is simply a payment for branding, which seems quaint in the domain of open contracts.
Preliminaries
The canonical AMM is based on two formulas. First, the price is represented by the ratio of the tokens in the pool. For example, with 1500 USD stablecoins and 1 ETH, the price would be 1500, which is common sense.
Secondly, for an existing pool, a trade with ETH going in and USD going out is subject to the following rule: the product of both tokens must be maintained at its existing level, a constant.
While this model works, unrestricted ranges are capital inefficient. For example, if you wanted sufficient liquidity so that a $10K order would move the price of a token priced at $1500 by 0.1%, you need $40 million in ETH and USDC in the pool. This is insanely inefficient for stablecoins, where 99.999% of the time, prices are locked at parity.
In May 2021, Uniswap released v3, allowing users to provide restricted or concentrated ranges. I describe the mathematics of v3 in this post here. With v3, you use the same foundational equations above but have to adjust individual LP USD and ETH pool quantities to reflect their particular ranges and also track the vector of total liquidity provided across all possible prices.
One can see the capital efficiency by noting how much capital is required to provide the same amount of liquidity for various ranges. Below we see how much capital is needed as a percent of the unrestricted range (i.e., v2) for range sizes.
Figure 1
Relative Capital For Symmetric Restricted Ranges of Various Sizes
Same liquidity
* e.g., a 10% spread for a token priced at 100 would have bounds at 90 and 111 (i.e., 100/0.9)
As shown above, a stablecoin pair where an LP offers liquidity between 99.9 and 100.1 can provide 0.05% of the capital for the same amount of ‘liquidity.’ This v3 pool would be 2000x more capital efficient than v2.
For pairs with risky tokens, like ETH/USDC, a range covering 15% up or down corresponds to about a week’s volatility. An LP receives fees only while the current price is within its range, defined as an ‘active’ range. If one wanted to be 95% sure their range would be active after a week of neglect, a token like ETH with an annual volatility of 90% needs a 30% range, which requires only 15% of the capital of a v2 range.
While the market price can breach all restricted ranges, such a case generates no risk to users; the pool would merely become irrelevant. There would be no trades so that the LPs would generate no trading fees, but neither LPs nor traders would have credit risk. A pool where all the LP ranges were inactive would be like if there were a venue where one could buy Bitcoin for $100k; no one would use it. In v3, the total absence of active ranges is rare because other LPs arise to capture fee revenue; the first to provide liquidity with a dynamic range would get 100% of fee revenue.
Alternative
Uniswap’s concentrated range is not the only way to economize on LP capital. Indeed, as a v3-style approach capital efficiency is absent off the blockchain, it is not the simplest way to leverage capital. While admirably clever, it is a product of path dependence, aiming to maintain the standard functionality of v2 by adding several parameters. Leverage, or its converse margin, is the common traditional finance method. Remember that leverage and margin are just two sides of the same coin, in that maximum leverage of 8 implies a 12.5% required margin.
Consider the case where Alice provides liquidity for a range covering the current price by +/- 10% with the same liquidity as an unrestricted pool (hereafter, ‘v2’). Below the v2 case is presented as a special case of v3 where the range is infinite (zero to infinity). The capital needed for the v3 range is about 5% of that required for a v2 pool, consistent with Figure 1 above.
Figure 2
Alice’s v3 LP vs. a v2 LP with the Same Liquidity
We can replicate the v3 capital savings via leverage, which implies giving the LP an asset and liability. Assume Bob provides 1.32 ETH and 1987 USDC in a leveraged v2 pool, the same token amounts Alice provided in her v3 pool. Here Bob would need to borrow ‘25.82 - 1.32’ (24.49) ETH, and also 36,742 USD. Instead of Alice’s extra account parameters pLow and pHigh, Bob has the additional account parameters corresponding to the ETH and USDC he borrowed to establish his v2 range. For Alice in her v3 range, and Bob in his levered v2 range, their account parameters look like this:
Figure 3
Bob borrows 24.49 ETH so that in addition to his initial ETH deposit, he has the right amount of ETH in the pool (and the same for USDC). This is reflected as a debit in his account labeled ‘vETH.’ Initially, his borrowing does not affect his account’s market value; it creates a symmetric asset and liability that cancels out. Bob’s net or ‘real’ ETH is 1.32, just like for Alice.
They have identical net amounts of ETH and USDC in their accounts, supporting the exact same amount of liquidity. As the price changes, this implies changes to their pool amounts, which in both cases are fictive numbers representing the implied amounts for a v2 pool. The pool amounts are levered LP Bob’s assets. As long as the price is within Alice’s range, Alice and Bob will have identical LP account values and thus also PnLs. This implies their impermanent loss (IL) will also be identical.
Figure 4
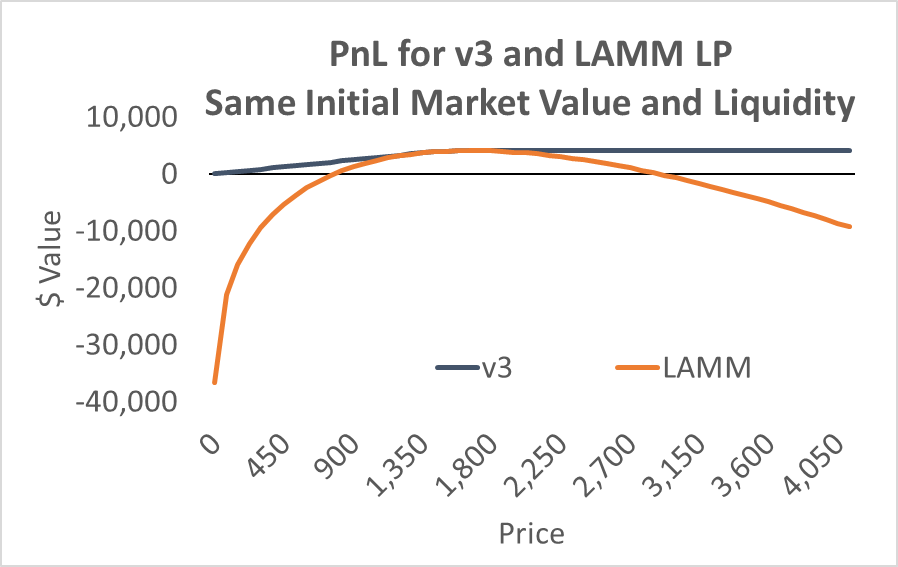
The difference between the PnL and the IL is the effect of the initial 1.32 ETH invested. Given their initial investment of $3975, Alice and Bob have an identical account value at the inception ETH price of $1500. The approaches generate identical PnLs across Alice’s v3 price range.
Over a broader price range, however, these approaches differ significantly. This is because Alice’s portfolio positions are static outside her price bounds. Bob’s levered position, however, changes continuously so that his account value becomes negative when prices move significantly up or down. [This all ignores fee revenue to make the presentation simpler.]
Figure 5
While Bob’s levered position is riskier over the infinite price range, the difference between Alice and Bob is slight over a broad price range from $1000 to $2000. Indeed, as noted for Figure 5 above, their PnLs are identical when the price is within Alice’s range of $1350 to $1667.
Bob’s potential for a negative account value, insolvency, implies a liquidation method is needed to protect the levered pool because if one party has a negative account value, not all accounts will be able to retrieve their full account values. Insolvency without any insurance fund would generate a run as those with assets in the pool would want to withdraw early enough to get their total account value; with an insurance fund, the equity owners would suffer a loss.
In the above example, we have 20x leverage given to LP Bob in that his pool ETH and USDC are about 20 times his initial ‘real’ ETH and USDC deposits. Leverage applied to an LP is very different than giving that to a trader. LP Bob’s account becomes insolvent at price moves of -50% and +95%, while a trader with 20x leverage would lose all of his money with a mere 5% price move. As the daily volatility of ETH is 5%, the protocol has adequate time to anticipate and rectify potential insolvencies before they are realized.
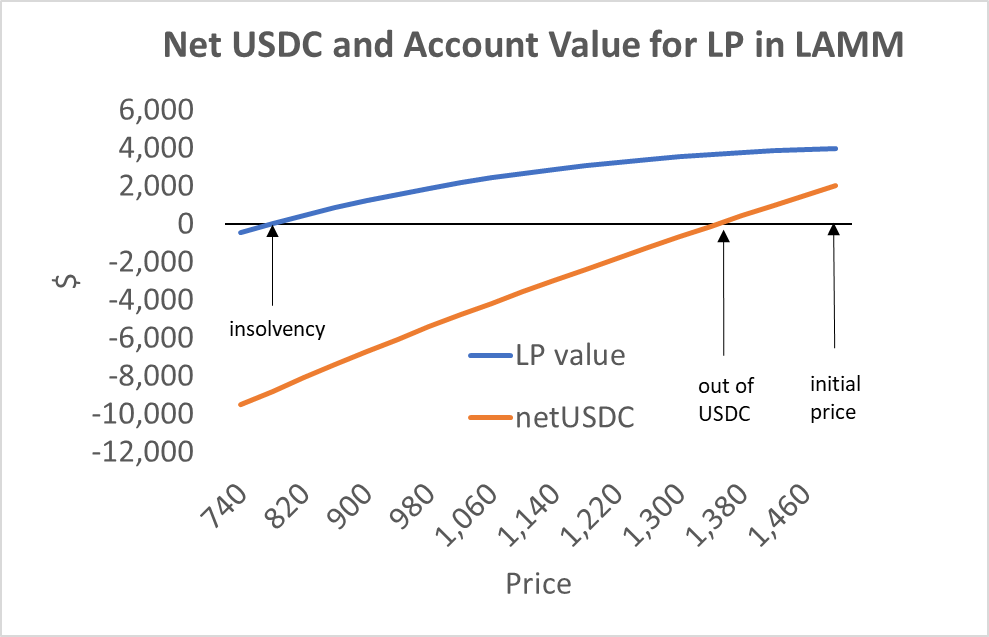
As a practical matter, however, a LAMM will be more concerned with LP token deficits rather than insolvency. As Bob matched Alice’s 10% range with his initial token allocation, a +10% price move would exhaust his ETH, and a -10% move would drain his USDC. At the price point of $1350 in Figure 6 below, Bob has zero net USDC, just like Alice.
Figure 6
While Bob has no more USDC to give out when the price of ETH falls to $1350, the value of his account is $3674, a loss of only $301, or 7.5%. Thus, well before the price moves that would render a LAMM LP insolvent, the protocol needs a mechanism for either motivating Bob to add tokens or incenting new LPs to add tokens so that swaps can resume.
A price where the LPs have net nonpositive USDC, such as $1350 in this example, implies no swaps can occur below this price. As with v3, this is not a danger to anyone, just a lost opportunity. Unlike the v3 case, new LPs will not get all the fees if they rectify this situation but instead share this fee revenue pro-rata with the existing LPs. This weakens the incentive for providing essential additional liquidity in the LAMM without some extra mechanism.
As a practical matter, there will be several, if not hundreds, of LPs, each with different starting price points and so each with different net token amounts. One LP with a net negative USDC would probably not mean the LPs as a whole have a net negative USDC balance. It is not essential to immediately liquidate an LP with a negative net token position, as the contract will still probably have positive net amounts of both tokens. This implies the rule for liquidation need not assume a single LP’s net token deficit implies a complete token deficit. For example, Bob could be liquidated when his net USDC fell below -1000, as opposed to 0.
Remember that in v3, the pool can also run out of a token if the price exceeds all LP ranges; historically, this has not been a significant problem. As the LAMM has weaker incentives for adding liquidity when the pool is out of a token, the key is creating incentives so this situation would be as rare as we see with v3 pools. This is a problem with several solutions.
Mechanisms for Incenting LPs to Maintain Positive Token Positions
An LP liquidation would be seamless in that no large trade is needed. An LP liquidation simply takes the ‘pool’ ETH and USDC implied by his liquidity given the current contract price, adds it to his vETH and vUSDC accounts, and zeros out his LP liquidity. The LP is left with an account with a positive value but deficient in one of the tokens. The contract could require the LP to have non-negative ETH and USDC balances before withdrawing his tokens. In the example below, the price has fallen to $1300, giving Bob a deficit of 686.83 USDC. Bob would be incentivized to deposit an additional 686.83 USDC in the contract, allowing him to withdraw his 3.24 ETH (worth $4,212). Once removed, the situation would be like when a v3 pool has no active ranges: no risk for anyone, just an opportunity for new LPs.
Figure 7
One solution would allow new LPs to remove deficient LPs when adding liquidity simultaneously. For example, a new LP could specify an existing LP deficient in one of the tokens at the time of adding liquidity. The contract would check to validate the LP was in default, then liquidate the LP while adding the new LP (here, default is triggered by a minimum net token balance, as opposed to the usual market value vs. required margin). This would give the new LP a greater incentive to rectify the problem, as it would make the situation identical to v3, where new LPs are incented by the lure of 100% of fee revenue.
Alternatively, one could emphasize the cost of the deficient LPs by giving keepers an incentive fee to liquidate LPs who are deficient in one token. This would be like the above condition, but with a different agent policing the contract for deficient LPs and a more prominent cost applied to these defaulting LPs. One could add that a liquidator must also rectify the liquidated LPs deficient token balance (which would require giving the liquidator an equal value of the defaulting LP’s surplus token).
Another solution would apply a funding rate based on the total LP’s net ETH and USDC. This would be a profoundly different application of the funding rate commonly used in perps, where the perp price is compared to an external spot price. One could use various functions, but the gist would be that the cost applied to deficient LPs would increase exponentially as the contract’s net ETH or USDC approached zero, giving LPs an incentive to add the deficient token.
Leveraged Traders: Perps
The leveraged LP has pool tokens implied by his liquidity and a corresponding debt reflecting his leverage so that his real or net ETH balance is the sum of these two accounts.1 If we treat his vETH account not merely as a debt but as a general trade account that can be negative or positive, traders could get leverage in the exact same way. The liquidation and accounting mechanisms would already be in place.
For example, trader Bob could deposit $750 USDC into the contract, generating the following account profile on contract.
Figure 8
Assume Bob then sells 1.0 ETH. Assuming no fees or price impact and a margin requirement of 20% (i.e., 5x leverage max), this would generate the following account data.
Figure 9
Alternatively, trader Alice could deposit $375 worth of ETH
Figure 10
If she shorted 1.375 ETH, her account would look identical to Bob’s in figure 9.
Or consider the case where a trader deposits 1 ETH and goes long 2 ETH, shown in Figure 11 below. His account would look like this:
Figure 11
One need only monitor whether the trader’s account market value exceeds his required margin, regardless of whether they are long or short. As long as traders cannot withdraw more than their required margin, and there is a mechanism and incentive for liquidators to liquidate defaulting accounts when they violate their required margin, the contract is safe.
Leveraged trading would allow the contract to function in a limited sense until some LP rectified the pool USDC deficit by depositing USDC. That is, while the contract has no USDC, traders cannot sell ETH for USDC as a swap, but those with collateral could sell ETH on the contract, generating a credit to their USD balance. A liquidation rule or funding rate approach will incentivize the existing LPs to shore up their balances soon, at which time the trader could withdraw their USD credit as USDC.
No Oracle-based Funding Rate
By having both Uniswap and perp functionality, the contract price would be set by arbitrage, not a funding rate linked to an oracle. This would eliminate several problems in perp protocols. Oracles needed for standard perp funding rate calculations can be hacked and censored. More importantly, the funding rate mechanism used to link perp prices with spot prices is a farce in that it is profoundly different than the funding rates applied in traditional swap markets or the basis in futures markets.
The Funding Rate Farce
In prime broker swap accounts, the funding rate is completely independent of the price; the assets in these accounts trade on spot markets as if they were not in swap accounts (you cannot tell which trades on the NYSE were made from swap accounts). Swap funding rates change slowly like general interest rates, are known ex-ante, and only apply to overnight positions. There is no reason to apply intraday funding rates because it is a pointless extension, as the magnitudes are too small to incent behavior meaningfully.
In futures markets, the difference between the futures and spot price is called the basis. It converges to zero at maturity, and as the futures moves toward the spot price over time, its change acts as a funding rate. This basis, however, is orders of magnitude greater than the usual 0.03% price premiums in perp markets. This larger basis allows for real arbitrage because it covers transaction costs and can be locked in. In contrast, in perp markets, the perp premium at the time of trade means almost nothing, as the funding rate is a function of the average perp premium over a position’s duration, not its value at the time the trade was initiated.
A perp price is set by a Schelling point, in that the most obvious target is the spot price, and the funding rate is just there to make traders feel comfortable that it is not merely a Schelling point. The fact that there is a vague relation to an equilibrating mechanism seemed a necessary and sufficient condition for perp markets when users had only one coin in the protocol, as was the case with BitMex in 2016. However, when trading ETH for USDC, this mechanism is an anachronism: let real arbitrage set the price.
The perp premium funding rate mechanism is incoherent and used to fleece traders whenever they are drunk with house money. If the market has just gone up, many ETH holders are sitting on big gains, so they do not mind paying an extra 5% for a month (aka only 0.018% every 8 hours). If your perp protocol has a funding rate based on its perp price premium to the spot, your perp protocol managers are either ignorant or evil.
StableCoin
An ETH-USDC contract with perp and Uniswap functionality naturally produce a stablecoin. Consider a user who deposits 0.375 ETH, where the ETH price is $2000. Her account value and required margin would look as follows:
Figure 12
Assume the trader goes long 0.625 ETH using leverage. Her account value would look like this:
Figure 13
As she is long $2000 worth of ETH, she needs 20% of that value in her account to satisfy her margin requirement.
Now consider Bob, who deposits 1 ETH in the contract. His initial account value would look like this:
Figure 14
He also has a $400 required margin, but as his position is not leveraged, it is never a concern. This is because if the value of ETH goes down, so does his margin requirement, and vice versa.
Bob can turn this into a MakerDao-like CDP position by withdrawing a new stablecoin, vUSD. Such a coin would be worth USDC within the contract, both adding to a user’s USD account when deposited, subtracting from the USD when negative. Yet the stablecoin would help economize on the contract’s USDC. By giving users cheaper fees when withdrawing a new vUSD stablecoin instead of USDC, a user would be incentivized to withdraw vUSD instead of USDC. The ultimate fungibility of USDC into vUSD on the contract would set the value of vUSD at parity with USDC as long as the contract is solvent. A withdrawal of $1250 vUSD would leave Bob’s account looking like Figure 15 below:
Figure 15
Bob’s account is exactly the same as Alice’s, though they arrived via different trades. A MakerDao CDP that generates a stablecoin is identical to a levered long position collateralized by ETH. A LAMM with swap and perp functionality makes stablecoins the way a donut maker makes donut holes, it’s an unavoidable complementary product. Just as it would be inefficient to produce donut holes but not donuts, it would be inefficient to produce stablecoins without a perp contract.
The benefit of this approach is that it creates stablecoins more efficiently because, unlike MakerDao, it does not rely on auctions or oracles. Auctions can be gamed, as when MakerDao sold $8MM worth of ETH in March 2020 for zero USD. In a LAMM, a defaulter’s net ETH position is straightforward to close on the contract. Relying on oracles is also problematic, as these can be hacked or censored.
In the long run, one could have several independent contracts, each with its own stablecoin. For example, a vUSD2 for a WBTC-USDC contract and a vUSD3 for a UNI-USDC contract. These other stablecoins would be supported solely by their specific LAMM contract, independent. Eventually, if one of these stablecoins became popular and used like USDC for transacting with several other contracts or products, it could act as if it were USDC. Like the creation of fiat money or valuation in new tokens, use eventually implies real value even if no ‘real’ assets are backing the token. Eliminating centralized stablecoins such as USDC from the blockchain is essential for long-run security. The creation of efficient decentralized stablecoin mechanisms is essential for that objective.
In summary
- Leveraged AMMs can economize on capital like restricted ranges
- LAMMs naturally extend to provide perps and stablecoins
- Current Perp Markets are Censorable and Gamed
- Perps on low-latency platforms are effectively centralized
- The BitMex-style funding rate equilibrating mechanism is a farce; it does not and cannot equilibrate the perp market
- funding rates are manipulated to benefit insiders
- see my prior post for an explanation
- A LAMM generates perps supported by real arbitrage
- Existing Stablecoins Not Sustainable
- Most centralized, fine for now, but not a long-run solution
- Decentralized stablecoins have regulatory attack surfaces
- Identifiable persons with control over choke points
- Oracles like Chainlink are censorable
- Governance tokens have weak revenue endgames
- incentive to embrace regulations when token growth stops
- A LAMM generates stablecoins without centralized attack surfaces
Concentrated liquidity in AMMs is a great innovation but ultimately ephemeral because it is inefficient. If there are ways to generate the same leverage but with more functionality, those will be adopted. There are many overvalued Ethereum tokens, and it would be nice to be able to short these on-chain, not just sell them. It would be nice to be able to short BTC or ETH, or take a position on BTC/ETH on-chain. None of this is feasible with only Uniswap pool functionality.
Shorting would benefit the Ethereum ecosystem because Ponzi tokens are a systemic threat in that they are common and run by stupid or evil people taking advantage of new crypto investors. These crap-coins sully the reputation of everything on the blockchain. It is much harder for insiders to maintain the value of a Ponzi token when people can short.
Yield farming highlights how inefficient many liquidity positions are because if collateral can be used elsewhere, that implies it is not used efficiently. If we ignore transaction and information costs, using LP tokens as collateral on other platforms is efficient; in practice, these costs are significant. For example, if you could use your house down payment to collateralize a car loan, your car lender would be better off requiring less collateral in cash. This is because lenders specialize in certain assets and are not efficient at monitoring the value of every asset one could apply collateral to and then making transactions in these other markets. A car seller would prefer you take out an additional home equity loan and give them the cash as collateral for a car loan, allowing the car seller to avoid building the infrastructure to monitor and potentially seize a person’s house.
This post is already too long for most readers, so I will not outline the best part of this approach, which is how it facilitates a mechanism to eliminate impermanent loss. Maybe later.
LP(i) net ETH = vETH + liquidity(i)/sqrt(price); net USD = vUSD + liquidity(i)*sqrt(price)


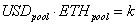






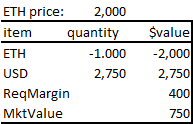
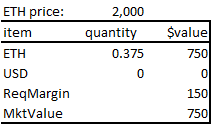
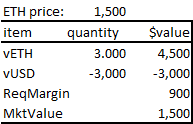




No comments:
Post a Comment