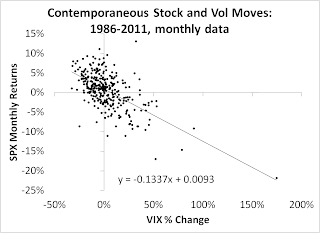
If you look at implied volatility, or actual volatility, it goes up when markets decline, and falls when markets increase. The reigning best explanation is that since most companies have some amount of debt, bad news increases leverage as the firm values fall, and higher leveraged firms have higher equity volatility, ceteris paribus. While this 'Merton model' explanation explains a little of what's going one, it probably doesn't explain that much in practice. I mean, it's not as if a Merton model helps predict equity volatility, even though KMV likes to convince its clients this is one of their valuable special tactics in predicting firm distress (don't believe them).
John Geanakoplos has been interested in leverage and business cycles (I noted his lecture below). Along the way he noted that there isn't really good theory for the stylized fact that volatility tends to go up when markets go down. Why should volatility be contemporaneously correlated with market declines rather than market climbs?
His theory is as follows: because people lever up more on assets that have higher bad news/high volatility correlations, because such assets don't fall much after the bad news, because so there is still a lot of uncertainty to resolve. Investors prefer such assets with negative news/volatility correlations because they can lever them more.
Now, this argument is tenable only under the cover of a complex setup using real analysis, so that the simple argument being made seems like Godel's incompleteness theorem. Yet, the answer is simply baked into his assumption of how various assets generate payoffs, and so has this faux-endogeneity that economists love. You see, endogenous results come out of the math (supposedly), there's no assuming the result, whereas 'exogenous results' are simply assumptions. Of course, these models have their exogeneity hidden in the rigged set up (note his asset payoff trees), which is as convoluted and artificial as any mathematical treatise on spherical horses moving through a vacuum.
Myself, I prefer the simpler theory. When times are good you simply do more of what you did yesterday, because that was good and you want more of it. There is little uncertainty in doing more. When things are bad--eg, you are losing money, or can't borrow any more--then you need to do something different, you can't afford to do what you did yesterday. As they say, things always end badly, otherwise they wouldn't end. There is a lot of uncertainty in doing things different, because there are now a bazillion things that you could do. Thus, bad news brings more uncertainty because it implies change, and good news bring lower uncertainty because it implies repetition.
Now, that won't make it to JET (the most rigorous of the esteemed economic journals) like Geanakoplos's paper, but it's truly a better theory.
John Geanakoplos has been interested in leverage and business cycles (I noted his lecture below). Along the way he noted that there isn't really good theory for the stylized fact that volatility tends to go up when markets go down. Why should volatility be contemporaneously correlated with market declines rather than market climbs?
His theory is as follows: because people lever up more on assets that have higher bad news/high volatility correlations, because such assets don't fall much after the bad news, because so there is still a lot of uncertainty to resolve. Investors prefer such assets with negative news/volatility correlations because they can lever them more.
Now, this argument is tenable only under the cover of a complex setup using real analysis, so that the simple argument being made seems like Godel's incompleteness theorem. Yet, the answer is simply baked into his assumption of how various assets generate payoffs, and so has this faux-endogeneity that economists love. You see, endogenous results come out of the math (supposedly), there's no assuming the result, whereas 'exogenous results' are simply assumptions. Of course, these models have their exogeneity hidden in the rigged set up (note his asset payoff trees), which is as convoluted and artificial as any mathematical treatise on spherical horses moving through a vacuum.
Myself, I prefer the simpler theory. When times are good you simply do more of what you did yesterday, because that was good and you want more of it. There is little uncertainty in doing more. When things are bad--eg, you are losing money, or can't borrow any more--then you need to do something different, you can't afford to do what you did yesterday. As they say, things always end badly, otherwise they wouldn't end. There is a lot of uncertainty in doing things different, because there are now a bazillion things that you could do. Thus, bad news brings more uncertainty because it implies change, and good news bring lower uncertainty because it implies repetition.
Now, that won't make it to JET (the most rigorous of the esteemed economic journals) like Geanakoplos's paper, but it's truly a better theory.
10 comments:
Looking at contemporaneous correlations of volatility changes and returns may be misleading since future volatility is fairly predictable from past volatility.
Serial correlation in volatility provides a straightforward explanation for the contemporaneous negative correlation of returns and volatility changes.
Current returns are negative so future returns will be higher to compensate buyers for the increase in expected volatility. Or buyers are entitled to a discount for holding a riskier asset.
Geanokopoulos's explanation is odd as it assumes negative serial correlation in returns which is not always the case in the data.
Your explanation fits with the above risk/return story, if you define bad times as increased past volatility. But you seem to define bad times as poor past returns. My instinct here is that in general increased volatility leads returns down and not vice versa. But I'm not sure what the data shows.
This correlation has always bothered me too – but I think the answer is even simpler – it’s a labeling problem. “Volatility” isn’t what’s being measured here, plain old uncertainty is and generally an upward bias in the markets is the norm. Your theory works too I guess because it also suggests that “times are good” is the default setting – which has been true enough in the modern finance era. Markets have generally had the wind at their backs (post WW II): most market participants and the mechanics of the markets themselves are biased to the upside. The whole purpose of the US capital markets (cue patriotic music) is to foster economic growth -UP. Cold calculations of value and price discovery via a fair and transparent marketplace are the main mechanisms to facilitate this but big picture-wise the later is in service to the former. Government market intervention also tends to be on the bid side. Add in a background of 100yrs. of $US inflation and: normal = up and up is more certain, all else being equal.
Outside of financial markets, “volatility” implies erratic, unpredictable or sudden action in an unknown direction but we know (as you describe) that up is less “volatile” as measured by option pricing than down (even if neither movement is particularly “volatile” in the above sense). So, maybe “fear index” or “uncertainty gauge” is actually a more accurate description of what is being measured.
Anyone can see that more uncertainty is associated with down than up because markets tend not to make sudden, massive up moves like they can/do to the downside. And most of the sudden, big upside moves that there have been in market history have probably all been preceded by big, sudden legs down (bounces essentially). At any give time the S&P 500 (for instance) is probably more likely to drop 10% than pop 10% in a single day even though the long term bias is up. This means higher options prices and thus a greater impact on the VIX etc.
Is there another gauge that measures only absolute percentage price movements and not derivatives prices? – that would reflect something more true to the term “volatility” -no?
Apologies for my previous comment confusing changes in volatility with the level of volatility. And while the level of volatility is predictive of the level of future volatility, the risk return argument depends on serial correlation in the changes and that is no doubt less strong with even daily data and likely not present at all in monthly data.
So in a monthly time-frame, your explanation seems to make much more sense than Geanokopolous's as he needs to have negative serial correlation in monthly returns which from my experience only shows up in daily or weekly returns.
Isn't it just the speed of falls tend to be much faster than the feed of increases?
People are fairly optimistic by nature. So most stocks are fully valued at most times, and so for the price to rise, something good has to happen in the real world (which is slow). When there's a hiccup, for the price to fall, the only thing that has to happen is that info has to spread (which is fast).
All plausible answers. Economics is a soft science. What's taken as truth today is heresy tomorrow.
I always use Mr. Occam as the tie breaker. Great post.
Implied volatility is partly a prediciton of future realized volatility, but also partly simply the cost of buying insurance. If people's desire for insurance goes up, with no change in their actual forecast of future volatilty, won't implied volatility go up now?
Can't that explain the relationship? When things fall people (rationally or irrationally) want more insurance?
Also, empirically, without really understanding why (at least I don't), marginal to the VIX, future realized vol is negatively related to prior return.
implied going up as a price of insurance would work, except actual volatility rises too. So it's not like the volatility 'premium' rises
People are reluctant to believe in miracles, but quite comfortable believing in disasters.
Like Mercury above, this correlation has bothered me too, and I agree that the VIX isn't actually measuring volatility as we normally would think about it. While Ken has a good point regarding discontinuous jumps being more likely to the downside - I think the real story is just a risk story. There is risk aversion baked into the discount rate Mr Market wants to use on future corporate earnings. When risk aversion abates - everything else being equal - the market rallies and the VIX simultaneously drops. When people start to get nervous, the discount rate increases, risk goes "off", markets fall, and the VIX rallies.
Post a Comment