On Tuesday, I argued that the main reason why perps do not dominate spot markets, as in TradFi, is that big players rightfully do not trust them for the following reasons:
LOB perps have to be centralized to lower costs and latency, creating a huge incentive for insider preferential access with no accountability
The prevalence of pump-and-dump tactics like staking, which, in the context of a perp governance token, has the sole purpose of reducing supply
No equilibrium theory justifies the 11% average perp funding rates
Perp funding rates uniquely rise after a rally and fall after bearish moves, unlike any TradFi futures market, taking advantage of bettor psychology
The academic work supposedly justifying the perp funding rate mechanism is profoundly different
Here, I want to add some data points provided by BitMEX perps. It highlights the market sentiment has nothing to do with equilibrium perp premiums, which makes sense because expected returns show up in the spot price, not the basis. We need grown-ups to take over, like when Walt took over Jesse’s lab on Breaking Bad.
First, it’s helpful to see the absurdity of the mechanism that presumably ties the perp price to the spot price. A perp is a derivative, and all derivative markets are built on an arbitrage, whether a futures or an option.
Define the Perp premium as the perp price over the spot price, in percent.
At the end of 8 hours, the average perp premium is translated into a funding rate debited by the longs and credited to the shorts.
Long FundingPayment(t+1) = - FundingRate(t+1) * Notional
Short FundingPayment(t+1) = + FundingRate(t+1) * Notional
FundingRate(t+1) = avg perpPremium (t to t+1) / 3
The story is that if the perp price is too high, it generates higher funding, encouraging shorts and discouraging longs, bringing the perp price back to the spot.
TradFi Futures Arbitrage vs. Perp Arbitrage
The main problem here is this is not arbitrage. With arbitrage, profits are certain. For example, in a futures market for oil with a standard fixed maturity (unlike a perp), the theoretical relationship between futures and spot is:
The futures premium, called the basis, is the difference in the interest rates of the traded asset to its numeraire interest rates. If one trades commodities, this is just the fiat interest rate minus the ‘own interest rate’ on the commodity (often negative, as it includes storage costs or decay).
To simplify the example, assume these interest rates are zero. In that case, if an arbitrageur sees the futures price above the spot price, he can lock in a profit by selling the futures and buying the spot. His payoff at maturity will be:
If Pfut0 > Pspot0
Payoff: longSpot + shortFutures
Substituting for starting and ending prices we have
Payoff: Pspot1 - Pspot0 + Pfut0 – Pfut1
Since at maturity, Pspot1 = Pfut1, the payoff is trivial, the known (i.e., constant) initial futures and spot prices.
Payoff: Pfut0 – Pspot0
This is a certain, riskless profit. Many people will be willing to lend to someone with access to a strategy that can make riskless profits, so this will be repeated until the futures and spot are equal.
Do while Pfut0 > Pspot0
Buy spot, sell fut
Endo
Arbitrage acts as a money pump on anyone defending a non-equilibrium basis, making markets efficient because there’s a limitless supply of capital for those with genuine arbitrage opportunities.
In contrast, in the perp market, we have a net payout of
+Pspott – Pperpt + Pperp0 - Pspot0 + fundrate
Here, the future price difference, Pspott – Pperpt, is not zero, as there is no delivery dictating equivalence. The perp premium could widen further, necessitating more margin or an early closure at a loss. Arbitrage will be tentative without the resolution we have in standard futures markets. There is too much risk to motivate unlimited capital into this opportunity. Further, the funding rate is not necessarily equal to Pperp0 - Pspot0. For example, in an 8-hour funding period where the prior 7-hour average perp premium was negative, the funding payment will probably be negative even if the current perp premium is positive. No one trading on funding rates would touch the perp until the next funding rate window, leaving the perp market unethered. Alternatively, the perp premium could widen further, necessitating more margin or an early closure at a loss.
A high funding rate does discourage longs and encourages shorts, but this applies to long-term investors. Such investors look over weeks, if not months, so they are not concerned by the minuscule edge on which market makers and short-term arbs are focused. For day traders, the uncertainties around potential 0.1% funding returns make the funding rate irrelevant, which is why they tolerate 50%+ funding rates (assuming a perp-spot arb, that’s 4 transactions, which would cost at least 20 basis point total, implying an unactionable range that implies funding rates with a 80% annualized range).
BitMEX Quanto Perp Premium Mainly a Covariance Estimate
In 2018, BitMEX offered a way to trade ETH with long and short leverage. People loved it then, and it’s still actively traded there today. As users only deposited Bitcoin, they had to be creative, so they created a bastard version of an FX quanto, which allows traders to, say, take a position on yen while staying in USD.
The BitMEX ETH-USD perp payoff is a notional amount times the change in the USD ETH price.
This is the platypus of perps with notional in Bitcoin and returns in USD. To translate into a pure USD return, we capture the change in value of the Bitcoin notional in USD from t to t+1. We can ignore the funding rate for the gist here, as the funding rate is determined elsewhere.
Translate from Bitcoin notional into USD at time t.
And then, once completed, back into USD
This way, the round trip starts and ends in USD
Rearranging we get
Using net returns:
The expected return of this ETH-USD perp is
Given that the ETH and BTC returns are about 80% correlated, this final term is significant and generates a convexity in the USD return.
The expected value of E(x*y) is the expected covariance of x and y.
I have intuition about volatilities and correlations, not so much on covariances. I prefer to replace this with correlations and volatilities to get the annualized covariance.
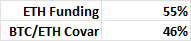
Since Jan 2019, the volatility for BTC and ETH has been 67% and 83%, respectively, with a correlation of 82%, generating a covariance adjustment that annualizes to be about 46%. The annualized return premium of the BitMex ETH swap compared to the ETH USD return over that period: 94% vs. 140% (all data reflecting arithmetically annualized returns applied to 8-hour intervals).
Annualized Arithmetic Returns
Jan 2019-May 2024
Interestingly, the average funding rate over this period was around 55%. This implies an average ETH-USD perp funding rate of 10% for the shorts, net of the boost provided by the covariance term.
Annualized ETH-USD BitMex Quanto Funding Rate and Covariance
Jan 2019-May 2024
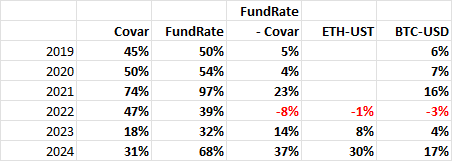
This highlights that those setting the BitMEX perp premium are good at their unpublicized objective. We see further evidence of the funding rate capturing the covariance by comparing the varying covariance with the funding rate over time. For example, when the covariance was very high in 2021, 74%, the funding rate averaged 94%, while when the covariance was low in 2023, 18%, the funding rate was 32%. The net funding rate, subtracting the covariance return, aligned with the ‘standard’ perp ETH and BTC funding rates over this period.
Annualized ETH-USD BitMex Quanto Funding Rates and Covariance
by Year
Another prime tell for manipulation is how the past, not the present or future, best explains the current funding rate. Here, I correlated the funding rate with three different returns, where P is the price of ETH in USD.
Funding rate: rate paid by longs at t+1 based on the average perp premium for an 8-hour window from t to t+1
Past return: Pt/Pt-3 days -1
Contemporaneous return: Pt+1/Pt -1
Future return: Pt+1+3days/Pt+1 -1
BitMEX ETH-USD quanto Perp Funding Rate Correlation
Jan 2019-May 2024
As funding rates are positively serially correlated, we should expect these to be the same sign. No equilibrium theory implies the past return to dominate the future or contemporaneous returns in explaining the current funding rate.
The Tether Yield Adjustment
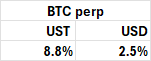
A final data point is provided by the difference between the BTC-USD perp denominated in tether, USDT, and the perp denominated in BTC. Those going long BTC-USDT post tether, while those going long BTC-USD post bitcoin.
As tether can be lent out at a 6% higher rate than BTC, this shows up in their average funding rates. This implies that the LPs are affiliated with the exchange, because somehow they have to getting the advantage of this higher yielding coin.
BitMEX BTC Perp Annualized Funding Rate by Numeraire
Jan 2019-May 2024
How Do Users Know This?
If the perp premium merely reflected sentiment, it would not capture the BTC-ETH covariance, as with the ETH-USD quant perp, nor would it accurately capture the opportunity cost on UST. No one on the web provides tools to incorporate these adjustments, though clearly the LPs are doing the correct adjustments. When I search ‘BitMEX perp funding rate covariance,’ half of the items presented are blog posts by myself over the past five years, implying I am a significant percentage of everyone in the world aware of this issue who can talk about it, a set that effectively rounds to zero. While BitMEX provides examples of how covariance affects the total returns given various hypothetical BTC-ETH returns, they do not offer simple tools to calculate this using current data.
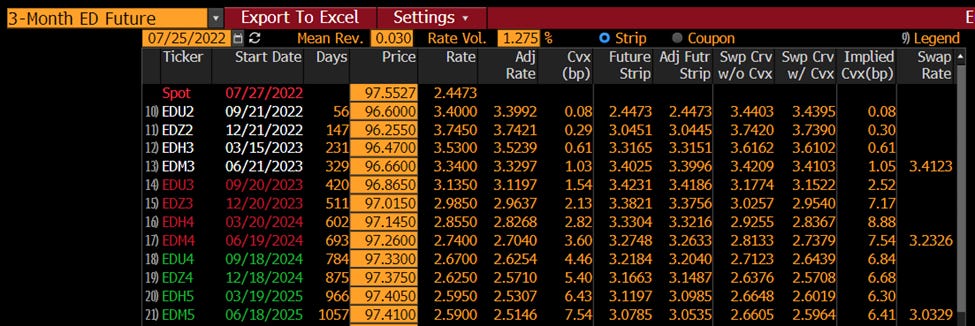
In traditional markets, convexity adjustments are explicit once known. The table above shows the detailed convexity adjustment needed when comparing Eurodollar futures with a Eurodollar swap. Before this relationship was understood, several large investment banks made actual arbitrage profits going long the futures and short the swaps. Around 1995, however, many prominent academic articles highlighted the arbitrage and noted the precise convexity adjustment needed. Eurodollar futures and swap traders all account for this subtle convexity adjustment, which is why such tools are ubiquitous.
BitMEX perp traders are oblivious to the current covariance or UST lending rate and just trade it like they would any other asset based on recent price movements. If the perp premium reflected bullishness, it would be quite a coincidence that bullishness correlated well with the recent ETH-BTC covariance. Those making markets, however, know what they are doing and are setting the perp premium to get their targeted funding rate.
BitMEX created perps out of necessity when there were no stablecoins. This anachronism persists because their LPs can profit from gaming this funding rate, as its typical users are generally trading noobs (who else would want 50+ leverage on an asset with a 60 vol?). Perp protocols will never dominate spot until they transition away from these sorts of cheap tricks, as institutions are rightfully wary of having significant positions on platforms that play silly games.
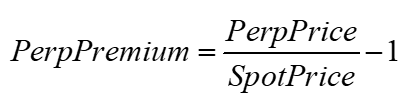
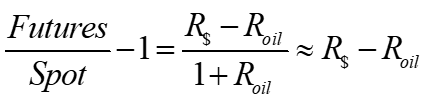
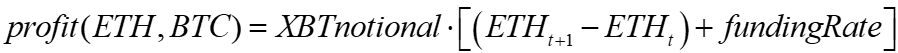
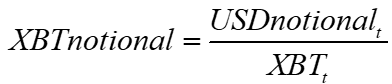
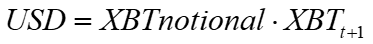
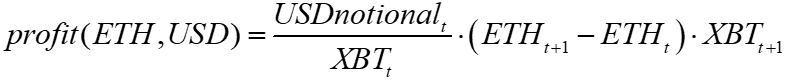
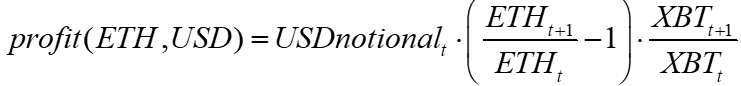
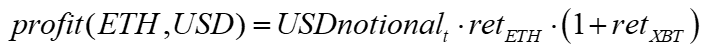

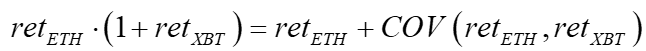
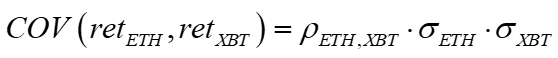


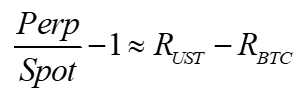
1 comment:
comment on wrong post, reposted here
"My pet theory is the perp funding rate is an estimate of the risk of exchange failure. Let's imagine a model LP that equal weights their capital across say 50 exchanges to harvest the funding (crypto-neutral).
How many exchanges vanish every year, or, equivalently, lock them out idiosyncratically for "reasons" in an impossible or hard to recover way? The equilibrium rate, where the LP does not make unreasonable profit, is the fundamental rate + the drag from exchanges regularly doing a runner.
Ballpark seems fine -- if anything it's probably too low, the market-implied exchange failure rate may be below the realized failure rate, given a constant influx of optimists!
It's same for DEX given risk of bug, hack, or the principals doing something naughty with the god key virtually all protocols have."
My response:
The longs are paying the above-equilibrium rate. Given that outsiders are generally long, they should get that risk premium, not the shorts, if there's a significant chance of an exchange default.
Post a Comment