Slavery is often considered a shining example of how "the moral arc of the universe is long, but it bends towards justice." Many people cannot understand how a worldview, or a 'real' God, could have any legitimacy today if it ever tolerated such an institution. I am a Christian, and while I agree that slavery is abhorrent today, it was a moral advance in its time. Those asserting that ancient tribes should have condemned it categorically are just naïve prigs.
Ancients had no moral qualms over what we today would consider horrific crimes. Members of outside tribes were so different in language, religions, and manners that they were considered beyond the universe of obligation they applied to their own tribe. For example, in Homer's Iliad, King Agamemnon explains why Troy will be annihilated.
"My dear Menelaus, why are you so wary of taking men's lives? Did the Trojans treat you as handsomely as that when they stayed in your house? No; we are not going to leave a single one of them alive, down to the babies in their mothers' wombs, not even they must live. The whole people must be wiped out of existence and none be left to think of them and shed a tear."
Genocide was not something anyone needed defending when dealing with vanquished foes. Ashoka the Great (280 BC) and Assyrian King Ashurnasirpal II (883 to 859 BC) boasted of genocide. When Rome razed Carthage in 46 BC, 150K Carthaginians were killed out of a total population of 200K to 400K. As late as 1850, the Comanche killed all adult males and babies in battles. When a tribe is at its Malthusian limit, its apologists will have no problem justifying such tactics.
Slavery or genocide was necessary because the survivors kept on fighting if released. For example, in 689 BC, the Assyrian King Sennacherib destroyed Babylon and carried a statue of their god Marduk back to Nineveh. By 612 BC, the Babylonians were strong enough to come back and destroy Nineveh, and the 2,000-year-old Assyrian kingdom never recovered. There were endless genocidal conflicts throughout the Bronze Age, so if a tribe, like the Hebrews, unilaterally chose to play nice and release captured soldiers, they would not have survived, and we would not even know about the Bible.
Unlike today, real existential crises existed all the time in ancient history. One of the worst genocides in human history happened in Britain and Ireland when invaders from Spain and France obliterated the natives around 2500 BC. This can be seen in that the frequency of the Y-chromosome G marker is now only about 1 percent, overtaken by those with the R1b marker, which makes up about 84% of Ireland's male population.
Around 2,500 BC, much of the European population's DNA was replaced with that of people from the steppe region near the Black and Caspian seas. This is a nice way of saying the men were killed. The Steppe Hypothesis holds that this group spread east into Asia and west into Europe at around the same time—and the current study shows that they made it to Iberia, too. Though 60 percent of the region's total DNA remained the same, the Y chromosomes of the inhabitants were almost entirely replaced by 2,000 BC. The history of humanity is not just the history of warfare but the genocides that accompanied it.
Slavery requires a society complex enough to have a formal justice system that enforces property rights, as highlighted by the many references to slavery in our oldest texts (Code of Hammurabi), law codes from 1700 to 2300 BC. It is an institution enforced not merely by the owner but by a community, as otherwise, enslaved people would run off at the first opportunity for a better life. Conquering tribes did not take the defeated men home and have them work as a group, they sold them off to individuals, diluting them sufficiently so that a slave uprising would be an impossible coordination task. Most people would prefer slavery to execution, however, making this a moral advance.
The feudal system applied to a continent united by a shared religion reduced the need for genocide or slavery in Europe. Serfs would serve their King regardless of which cousin won the job, and in either case, they would be allowed to worship the same god, so it did not matter too much. Yet the entire time, ethics were subject to prudential rationality. For example, ransoming captured nobility was financially prudent and honorable, but this principle was relaxed when costly, as all principles are. Thus, at the battle of Agincourt (1415), the English took so many prisoners that King Henry worried they might overpower their guards; he violated the rule of war by ordering the immediate execution of thousands. The selective application of principles in times of existential crises is rational and predictable (Cicero noted, "In times of war, laws fall silent.").
Prison is an invention of the early 1800s as an alternative to corporal punishment. Before that, jails existed merely to hold people until their trial, as no society could afford to house prisoners for a long time, which is why the death penalty was so prominent. As late as the 1700s, 222 crimes were punishable by death in Britain, including theft, cutting down a tree, and counterfeiting tax stamps. The alternatives, such as a fine or property forfeiture the average criminal did not have, and the non-punishment of criminals has never been an equilibrium. As Thomas Sowell has frequently noted, a policy must look at the trade-offs, not just the benefits, and these are often manifest in the alternatives.
In Knowledge, Evolution, and Society, Hayek argued that intellectuals do not create morals; they grow and sustain themselves via natural selection. John Maynard Smith applied this reasoning to animal behavior. He outlined that a strategy must work as an evolutionarily stable strategy, which involves iterated games where payoffs affect the distribution of players in the next game.
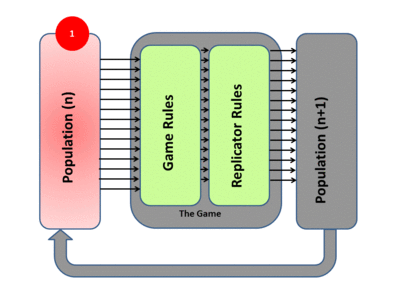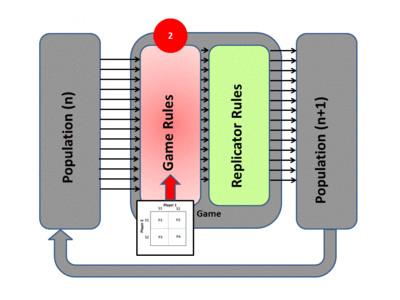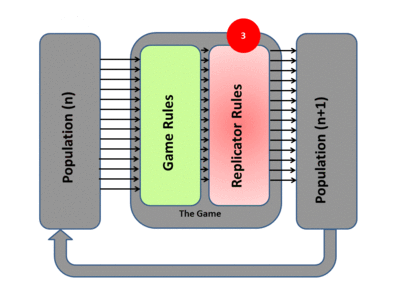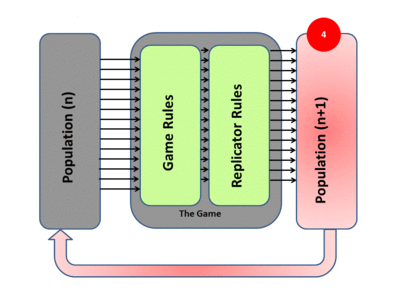 |
| Evolutionary Game Theory |
Mores, customs and laws must be consistent with strengthening the tribes that practice it, especially in the days when genocide was common. Productivity growth via social institutions like division of labor, or technologies like the plow, change the costs and benefits of human strategies. With more wealth, one can tolerate costs more easily, reducing the need for draconian punishment. This is a good argument for prioritizing policies that increase output over those targeting fanciful existential threats; wealthier societies can afford mores, customs, and laws that in a poor community would be irrelevant because they are infeasible.
The Bible laid the foundation for eliminating slavery once society could afford it. In the Bible, enslaved Christians are considered equal to their masters in moral worth (Gal. 3:28). Masters are to take care of their slaves, and slaves are encouraged to seek freedom (1 Cor. 7:21). In contrast, stoics of that time, like Seneca and Epictetus, never promoted manumission or the axiom that all men are made with equal moral status. They noted that slavers were also human, but this just implied slave owners should be nice to them, and Antebellum southerners were fond of quoting Seneca. The Philosophes of the 18th century, such as Rousseau or Kant, wrote almost nothing on the issue of slavery as practiced in their time.
The abolitionist movement only started in the late 18th century when English Christians (e.g., the Clapham Sect) and American Quakers began to question the morality of slavery. The principles underlying the condemnation of slavery revolve around the equality and dignity of all people. This was the primary motivational force of leading 18th Century British abolitionist William Wilberforce who viewed all people as "made in the image of God." This stands in contradiction to atheism which cannot justify nor defend the equality of humanity and its qualitative difference from any other sentient animal. While many Christians used the Bible to justify slavery, the more important point is that the seeds of slavery's eventual overthrow were based on Christian theology and championed by Christians, not secular philosophy and philosophers.
One can object to Christianity for many reasons, but it is ludicrous to suppose that slavery in the Bible proves it is morally bankrupt. If the Hebrews did not practice slavery, they either would have perished or had to have applied the viler tactic of genocide. If the first Christians campaigned for the immediate abolishment of slavery in an empire where 10-20% of the populace were slaves, the Roman government would have decimated them in the first century AD.
It is even more ludicrous to assert that because today's humanist intellectuals have never tolerated slavery, their worldview is morally superior to one based on a text written thousands of years ago that did. A mere century ago, humanist progressives were promoting colonialism, scientific racism, communist tyrannies, and fascism. Unlike slavery in the Bible, these were not the lesser evil policy given constraints of the time, but rather new policies foisted from above that increased human suffering and decreased human flourishing. To say that these errors were not 'real humanism' is special pleading.
Slavery was known in almost every ancient civilization. Outside of that sphere, slavery is rare among hunter-gatherer populations because it requires economic surpluses, the division of labor, and a high population density to be viable. Further, their social organization is too limited to create anything approaching a battalion, so they never engage in what one would call a war, and are thus never presented with the problem of what to do with one thousand enemy soldiers.