Uniswap V2 Made Money. What Happened?

 I was surprised to see a tweet by @AnthonyLeeZhang that referenced a short paper showing liquidity providers (LPs) making money on Uniswap's ETH-USDC pool, as I have noted that Uniswap LPs have been losing money consistently since they began. I initially thought there was a mistake, but found his metric of PNL is ultimately identical to mine. 

Specifically, he used Milionis, Moallemi, Roughgarden, and Zhang's pnl formulation, which they call Hedged LP PnL. This is the LP profit after accounting for impermanent loss (aka, loss vs. rebalancing, LvR, convexity costs).

HedgedLpPnL = fees - LvR = Vt - V(t-1) - mints + burns + hedgePnL

Here, V(t) is the value of the pool's reserves.  If we use the ETH-USDC pool, where p(t) is the ETH price is USDC, we get

V(t) = USDC(t) + ETH(t)*p(t)

V(t-1) = USDC(t-1) + ETH(t-1)*p(t-1)

The difference in the value of reserves is affected by the price change and the changes in USDC and ETH that come from mints (LP deposits), burns (LP withdrawals), trades, and fees. The ETH and USDC coming into the pool contain both fees and the tokens traders sell (swap into the pool), so this implies

USDC(t)=USDC(t-1) + mints(t, t-1) - burn(t, t-1) + NetUsdcIn(t, t-1)

ETH(t) = ETH(t-1) + mints(t, t-1) + burns(t, t-1) + NetEthIn(t, t-1)

[note: (t, t-1) is the flow in the period from t-1 to t]. This reduces to just valuing the pool's net USDC and ETH reflected in trader swap event logs, valued at the end of the period. There is a slight difference created by ignoring the prices when mints and burns happen, but both approaches make assumptions that make these PnL calculations approximations, and the differences are insignificant. I prefer this formulation because it requires less data.

Hedged LPpnl = NetUsdcIn(t, t-1) + NetEthIn(t, t-1)*p(t)

While one can use periods of arbitrary duration, in the limit, it does not matter, and as a practical matter, pulling this by calendar day works well for seeing trends, as well as avoiding trading costs if one were to actually hedge their LP pool position.  

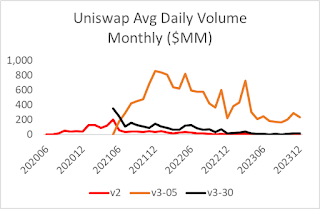
More importantly, this introduced me to the fact that Uniswap's v2, the old capital-inefficient automated market maker (AMM), makes money for its LPs. I figured it was obviously worse in every way, which is why its flagship ETH-USDC 30bp fee (basis points, 0.3%) pool has about 2% of the volume of the ETH-USDC 5bp v3 pool, which is about half of the unpopular 30bp v3 pool. 

ETH-USDC pools

Uniswap's v2 started in May 2020, and volume peaked when Uniswap's upgraded v3 pools started in May 2021.  Not only did their v2 LPs make money in the past, but they have continued to make LP profits to this day. In its first year, 2020, Uniswap's v2 pool was making $100k+ per day for the pool, which annualized to a sweet 30%+ annual return on total value locked in the pool (after accounting for impermanent loss/LvR/convexity costs). 

Uniswap v2 ETH-USDC pool

Currently, there is about $100MM worth of tokens in the ETH-USDC v2 pool, and it generates a modest, but still positive, 3% APY all-in. On a PnL/USD traded basis, it has been more impressive, showing stable profitability (see below). In contrast, the v3 pools have lost money from inception. While v3 LPs make money twice as many days as they lose money, the problem with selling gamma (having a negative convexity) is that the losses are relatively large when they happen. Unfortunately, this leads many scammers and fools to think that they only need to time or size their bets better.

ETH-USDC pools

This is quite an interesting equilibrium.  The 30bp-fee v3 pool corresponds to the 30bp-fee v2 pool, yet the v3 LPs lose money while the v2 LPs make money.  The problem is that the v3 pools have too much liquidity relative to the total amounts traded. If the pool is near the 'true' price as reflected on Binance, etc., standard fluctuations imply a certain amount of trading. Specifically, over short frequencies, the percent change in price relates to an amount traded relative to the liquidity. Remember that in an AMM liquidity is defined as

liquidity = sqrt(USDCinPool * ETHinPool)

Applying AMM math, we get

return% = 2 * DUSDC/(liquidity * sqrt(p))

If we take daily volatility to be 5%, the standard deviation every five minutes is 0.3%. If arbitrageurs pushed the price by an average of 0.3% every five minutes, that's a total of 85% that needs to be effected. This implies the amount traded for arbitrage or price setting is a linear function of liquidity.

DUSDC(from arbs) = 0.85 * liquidity * sqrt(p) / 2

If LPs need a certain ratio of liquidity traders relative to arbitrage traders, then if the ratio of (USDC traded / liquidity) is lower for a pool with the same fee, it will make less money, if not lose money. The 5bp pool needs at least 6 times more USDC traded per unit of liquidity. 

We see that for the v3 5 bp pool, volume/liquidity has been 2.5 times higher than in the v2 pool, far lower than the 6 times it needs. In the v3 30bp pool, the ratio is about 50% of the v2 pool. The flagship AMM for the flagship dapp on the flagship blockchain has been and continues to be a loser. This is an existential problem for AMMs because large users are constrained to centralized exchanges without a sustainable, liquid AMM. These centralized exchanges are necessary but cannot be essential for large trades if crypto is to avoid outside attacks by the institutions that control the major fiat currencies.

ETH-USDC pools

I can only speculate as to why v3 fails so spectacularly relative to the v2 AMM. I suspect the cause is based on LPs not appreciating LP convexity cost. If you scroll through Reddit's Uniswap thread, you will see occasional posts inquiring about how to measure or hedge the LP's negative convexity, and banter is similar to when college freshmen discuss macroeconomic issues: strong, ignorant opinions. Most do not even realize the convexity cost. Those who do acknowledge it think it can be overcome by judicious timing, lower latency, or rewards programs that solve the chicken-and-egg problem. Others think the solution is to buy volatility as a hedge, which in the context of the blockchain is not only capital inefficient (you can't get cross-collateralization), but if you are selling volatility below actual volatility as with these v3 LPs, hedging it on centralized exchanges will just lock in your losses. 

With the v2 pool, there is one common cost for the LPs they all can intuit: capital. Every LP is treated pro-rata based on their stake in the AMM's pool. In contrast, many v3 LPs think that they get ahead of their fellow LPs by concentrating their liquidity in a narrow band or adjusting their ranges based on current volatility. The effect of extra liquidity never occurs to them. The end result is a persistent excess of liquidity that does not just dilute profits; it turns them into losses. The greater the liquidity, the greater the convexity cost, which, unlike merely adding shares to a stock, affects the sign of net income. 

Many have written about how adding money to a v3 pool is obviously a better strategy than LPing for a v2 pool because by restricting a range to a generous 20% up and down, they could deploy the same amount of liquidity with only 8% of the capital they would need for a v2 pool. They never considered the consequences if everyone else came to the same conclusion, leading to an excess of liquidity that is linearly related to the pool's convexity cost. As most people do not understand, let alone measure, convexity costs, they blithely deposit capital into these pools, ignorant of the equilibrium effect on costs that affect their bottom line.

This unfortunate situation could persist in that my spam folder is filled with the same scams that were a cliche in the 1990s. Yet, while the weiner enlargement pill industry is persistent, it isn't growing. For a contract on the blockchain to work, it has to go beyond gimmicks like token rewards (which just dilute LP fees) or leverage via using collateral tokens as collateral ad infinitum. Unfortunately, the investors that generated massive profits in 2021 and avoided prosecution or bankruptcy--probably out of pure luck--are the primary VCs directing our current development. They have a lot of money they do not want to report and nothing else to do with it. They know the shibboleths but do not understand gamma in particular or mechanism design in general.