Budish's Plan to Replace CLOBs

I don't keep up with the latest economics journals because I've learned that very little of it is fruitful. Like many subjects, the basics are valuable, but the marginal returns are small with the exponential rise in academic output. We aren't in the golden age of economics if there ever was one.

Yet, I am still fond of economic models that illustrate a point clearly and succinctly, and I stumbled across a model that applies to an area where I have first-hand knowledge. I worked on high-frequency trading algorithms to execute our hedges for an electronic equity-options market maker. We were not at the bleeding edge of high-speed trading, so I am not privy to the tactics used by Renaissance, etc., but no one from those firms will talk about what they do anyway. If someone does talk about what they did, they are invariably a smokescreen.

Further, many high-frequency clients want stupid things, like different models for when the market is trending vs. staying in a range. This is a stupid idea because if one knew we were in a trading range, there would be better things to do than apply nuances to a VWAP algorithm. However, if customers want to pay for it, you might as well sell it, and the best snake-oil salesmen believe in their product. Thus, many great firms with access to the best of the best employ deluded people to create and sell such products, useful idiots. They often speak at conferences.

Experienced private sector people discussing bleeding-edge high-frequency traders (HFTs) are generally deluded or deceptive. This leaves a hole filled by people with no experience, like Michael Lewis. Thus, I am qualified as anyone who will talk about these matters, even if I am not and have never worked on a successful worm-hole arb-bot from New York to Tokyo. Indeed, one might say my experience in HFT was a failure, as we couldn't compete, and I was part of that. I haven't worked on that problem directly since 2013. However, like a second-stringer, I can better appreciate what doesn't work, which is easy to miss if you are making bank because you aren't constantly looking for ways to fix things.

Budish at a16z

Eric Budish is a professor at the University of Chicago and the coauthor of several papers on 'hedge fund sniping' on limit order books, most conspicuously Budish, Cramton, and Shim (2015), and Aquila, Budish, and O'Neill (2022). I do not want to dismiss his coauthors or put all the blame on Budish, but for simplicity, I will present this work as being Budish's singular work. This work has been popular, as it was mentioned in the press, sponsored by significant financial regulators like the FCA and BIS, and was the basis for talks last year at the NBER (here) and the crypto VC a16z (here).

His work highlights the best and worst parts of economics. He presents a model that highlights the assumptions required, the mechanism, and then tries to support it with data. That makes it subject to rational criticism, unlike most work in the social sciences. On the bad side, it follows in a tradition from Frederick Taylor, the original McKinsey/Harvard MBA, who wrote about Henry Ford's assembly line as if his analytical approach was relevant to a famous business method (assembly line) and generated insights into other areas. It doesn't. 

Budish's big insight is that a profound flaw in Centralized Limit Order Books (CLOBs) generates a deadweight loss. When HFTs compete on CLOBs, they often engage in speed races that inflict costs on LPs (aka, liquidity providers, market makers). What is new is that this form of adverse selection is not generated by asymmetric information but by the nature of the CLOB. If the top HFTs are within a Plank-length of each other as far as the exchange is concerned, the fastest is arbitrarily chosen. However, in high-frequency trading, the fastest wins, and the losers get nothing (a Glenn Gary-Glenn Ross tournament).

An HFT would only snipe the best bid or offer if it made them money, and for HFTs, this is a zero-sum game, so the poor liquidity provider suffers losses. While the LP can try to cancel, he is one, and those who are not him are more than one, so when thrown into the micro-second blender behind an exchanges gateway, the LP will lose the race to cancel before he gets sniped. In equilibrium, the LP passes that cost off to customers.

His solution is to replace the continuous limit order book with one with discrete auctions. This allows players to compete on price instead of time because, in each period, they will all be represented, not just the first one, and the snipers will compete away the profit that was generating a loss for the LP.

Primer on Adverse Selection

In standard models of LPs, there is the LP who sets bids and offers. He will buy your shares for 99 and sell them to you for 101, a two-sided market. Liquidity traders come along and buy at 101 and sell at 99. If we defined the spread as the difference between the bid and ask (101 – 99), the LP's spread is 2; his profit is spread/2, or the price relative to the mid. The LP's profit transacting with liquidity traders is the number of shares he trades times half the spread.

There are also informed traders with private information about the value of their assets in the future. This also goes by the phrase adverse selection because conditional upon trading, the LP loses money with informed traders. These LPs trades are selecting trades that are adverse to their bottom line.

But, the nice thing is that the informed traders discipline the LP, setting the price at its true market clearing price. Liquidity traders pay a fee to the LP via the spread for the convenience of instant transformation from cash into asset or vice versa. The LP has to balance the profits from the liquidity traders with the losses to the informed traders so that the benefits of liquidity traders offset the costs of adverse selection.

If we assume profits are zero, the greater the adverse selection, the greater the spread, but this is a real cost, so such is life. Information is costly to aggregate when dispersed unevenly across an economy. However, to the degree we can lower asymmetric information, we can lower the spread. In Budish's model, his toxic flow is not informed, just lucky, but the gist is that these traders are imparting adverse selection costs onto LPs just like informed traders in previous models.

Budish, Cramton, Shim model

I will simplify the BCS model to make it easier to read by removing notation and subtleties required in an academic journal but a distraction for my purposes. Hopefully, I will capture its essence without omitting any crucial subtleties. Let us define S as the spread, so S/2 is half the spread. This is the profit the LP makes off liquidity traders.[eg, if bid-ask is 99-101, the spread is 2 and S/2 is 1, so the profit per trade is 1].

 Let us define J as the absolute size of the price change that is revealed to the HFTs, a number larger than S/2. It can be positive or negative, but all that matters for the LP is its size relative to S/2, because the profit for the sniping HFT will be J – S/2 (eg, buys at p+S/2, now worth p+J, for a profit of J – S/2) and the LP loses (J - S/2). In the following trade, either J is revealed, a jump event, or it is not, and the liquidity trader trades. If the liquidity trader trades, the profit is S/2.

The next trade will come from a liquidity trader or a sniper. As the probability of the sum is 1, we can simplify this to being prob(jump) and 1-prob(jump). Assume there are N HFTs; one decides to be an LP, and the others decide to be snipers, picking off the LP who posts the resting limit orders if a jump event occurs. All of the HFTs are equally fast, so once their orders are sent to the exchange's firewall for processing, it is purely random which order gets slotted first. Thus, the sniper's expected profit each period is

That is, the probability of getting a signal, Pr(jump), times the profit, J – S/2, times the probability the sniper wins the lottery among his N peers.

For the LP, the main difference is that he only loses if the other HFTs snipe him. He tries to cancel, avoiding a loss and making zero. We can ignore that probability because it is multiplied by zero. But the probability he loses is (N-1)/N. This is the crucial point: The upside for snipers is small per sniper, as it is divided by 1/N, but it is large for the LP, multiplied by (N-1)/N. To this loss, we add the expected profit from the liquidity traders. The profitability of the LP is thus

The HFT chooses between being a sniper or an LP, where only one can be an LP. In equilibrium, the profitability of both roles must be equivalent.

 

Solving for S, we get

The profit should be zero in the standard case with perfect competition and symmetric information. The spread is positive even with symmetric information because the lottery is rigged against the LP. It seems we could devise a way to eliminate it, as it seems inefficient to have liquidity traders pay a spread when no one here is providing private or costly information. The 'hedge fund sniping' effect comes from the race conditions, in that any poor LP is exposed to losses in a jump event, as there are more snipers (N-1) than LPs (1).

When you add the costs of speed technology, such as the Chicago-New York fiber optic tunnel, these HFTs must recover this cost, which adds another nice result in that speed costs increase the spread. Now, we have the profitability of the sniper after investing in technology. Here, we will set the profitability of the sniping HFTs to zero.

This implies

Now we take the equilibrium condition that the profitability of the sniper equals the profitability of the LP

And while the c cancels out, we can replace Pr(jump)*(J – S/2) with C*N to get

In this case, the N is endogenous and would depend on the function c, so the spread is not exactly a linear function in c. Given the various flaws in this model discussed below, elaborating this result is not interesting. The main point is that S is positively related to C, which is intuitive. Again, even in the absence of asymmetric information, we have a large spread that seems arbitrary, which seems like an inefficiency economists can solve.

Data

Budish presents two sets of data to support his model. In 2014, he noted the occasional crossing of the SP500 futures (ES) in Chicago with the SPY index traded in New York. This arbitrage is famous because there have been a few times when HFTs spent hundreds of millions of dollars creating straighter lines between Chicago and New York, getting the latency down from 16 to 13 to 9, and currently, with microwaves, we are at five milliseconds. I don't think it's possible to get it down further, but weather can affect microwaves, so perhaps there is still money to be spent. In any case, it's a conspicuous expenditure that seems absurd to many.

There's a slight difference in the futures and the SPY ETF, but this is stable and effectively a constant over the day. The bottom line is that the correlation is effectively perfect over frequencies greater than a day. Over shorter durations, however, the correlations have been rising, and the correlation at one nanosecond has and will always be zero because the speed of light sets a lower bound on how quickly information can travel between Chicago and New York of 4ms. One can imagine various reasons why the markets could become disentangled briefly. Thus, when we look at prices over 250-millisecond intervals, there were periods, almost always less than 50 milliseconds, where it was possible to buy futures and sell the ETF for an instant profit. This did not happen frequently, but it generated arbitrage profits when it did.

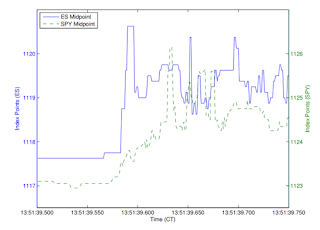ES vs. SPY over 250 ms

Buddish assumes traders can buy and sell the other whenever these markets cross for more than 4 milliseconds. In his 2015 paper, his data sample of 2005-2011 generated an average of 800 opportunities per day for an average profit of $79k per day.

In 2020, he presented data on the London Stock Exchange stocks and used it to estimate latency races cost investors $5B a year worldwide. It made quite a splash and was picked up by many prominent media outlets such as the Financial Times, Wall Street Journal, and CNBC. Unlike the ES-SPY data, this one does not involve strict arbitrage but statistical arbitrage. Using message data from 40 days from the LSE in the fall of 2015, they can see trades and cancellations and those transactions that were not executed because they were late. This gets at the cost of latency. Budish highlights that he can isolate orders sent at approximately the same time, where one order was executed merely due to chance, and all the others miss out. More importantly, the limit orders are sniped by the faster trades (which can be limit or IOC, immediate or cancel, orders that take liquidity), which is the essence of the BCS model.

He isolated clusters of orders within 500 microseconds, or 0.5 milliseconds, that targeted the same passive liquidity (quantity & price). Most data involved 3 trades, but only 10% included a cancel. As a failed take order implies no more quantity at this price, these were all relevant to taking out a small queue. For example, here's a hypothetical case where there is a small limit to buy at 99 and a larger offer to sell at 103, for a midprice of 101.

 

Note that if the sniper takes out the limit order to buy at 99, he sells below the midprice before and after the trade. As the sniper is selling here, they define 'price impact' as how much the mid moves after the trade in the direction of the trade, here, +1 unit; he pushes the price down by 1. The 'race profit' compares the trade price to the after-trade mid; in this case, it is -1 unit because the selling price of 99 is one unit below the new midprice of 100; his profit is -1.

A case where the sniper would profit could look like the figure below. Here, the sell moves the mid down by 2 in the direction of the trade for a price impact of +2. The race profit here is positive, as the sniper sold for 101, which is +1 over the new midprice.

 

 By definition, the price impact will be positive because it takes out the best bid or offer. If the best bid or offer remained, the sniper would not win the race, as there would be no loser.

Applied to their set of 40 days on liquid LSE stocks, they estimate these latency races are involved in 20% of all LSE volume. So, while they only last 79 microseconds, they apply to 1000 trades per ticker daily. They estimate an average race profit of 0.5 basis points on a set of stocks where the average spread is 3.0 basis points. Applying that to all stocks traded generates $5B.

Criticisms

I sense that no one criticizes this work much because it's a parochial problem involving data that requires money and a lot of time. As even economists specialize, and many do not examine CLOBs, they ignore the Murray Gell-Mann amnesia effect, so Michael Lewis's Flash Boys informs even academic economic opinion on this issue, as evidenced by Budish's frequent mention. The SBF debacle highlighted Lewis doesn't have the discernment to realize when he is dealing with complete frauds whose primary business was making markets, which should hopefully warn economists not to take Flash Boys seriously when trying to understand modern markets.

Either/Or vs. Both/And

My first issue is where the HFTs sort themselves into two roles: ex-ante, one chooses to be the liquidity provider, the others as stale-quote snipers. Most HFTs run a combo strategy of sniping and LPing. If we look at the scenario he outlines as sniping at the LSE, we can see that they are sniping aggressive quotes. An aggressive quote is essential for getting to the top of a queue and making money as an LP.

Generally, a resting order at the top of the queue has a positive value, while one at the bottom does not. Investing in speed infrastructure is the only way to get to the top of the queue. Consider the LOB below. Here, the top of the bid queue is in yellow at a price of 98. That queue position has a positive value. At the end of the queue, the position in dark blue generally has a negative value. While there are various scenarios where it pays to stay at the end, the bottom line is that you generally want to get to yellow, but to do so implies one first takes a stab at a new, aggressive level. The yellow ask at the price of 102 is how that happens.

 

As noted in their paper on the LSE, the top 3 firms win about 55% of races and lose about 66% of races. The figures for the top 6 firms combined are 82% and 87%.  Thus, getting to the top of a queue with several LPs is an important and probabilistic game. Budish did not look at those races. It seems they would most likely be competing for queues and, if they lose, sniping those queues. Both rely on a sizeable specialized investment.

Only a handful of firms are playing this game on the LSE in Budish's data, and they are playing with each other. To the extent the stale quotes are from other HFTs, they are playing a zero-sum game among themselves. However, likely, these stale quotes are usually from non-HFTs, such as retail traders with their E-Trade platforms. That most stale quotes are not in the HFT club is consistent with the fact that only 10% of Budish's data included cancel orders.

Even if we assume the sniping only affects fellow HFTs, the latency tax disappears when we think of them probabilistically sniping or posting resting limit orders. Assume each of N HFT traders has a 1/N chance of sniping the newest bid-ask level, which is necessary for getting to the top of the next queue, the cost of sniping cancels out. That is, there are two symmetric probabilities applied here, one to becoming the lead on a new tick, the other reacting to the jump event. The resulting equilibrium equation (without c) is just

 

So, when providing liquidity, the probability of getting sniped is (N-1)/N, but now this is multiplied by the probability of being on the new aggressive bid, 1/N; the probability of winning the snipe is 1/N, which is now multiplied by the probability of being a sniper, (N-1)/N. This cancels out the cost from the latency race, so it need not be passed off to liquidity traders via a spread. S=0. 

BCS states that it does not matter whether one always chooses to be the liquidity provider or they chooses so stochastically. I suspect they think it does not matter because the expected profit of posting liquidity and sniping is equal in equilibrium. However, that assumes the HFTs make a fresh decision as if they were certain to become the top of the next queue. In practice, they will have to try to be the lead LP on a queue, and their success will be stochastic, so they evaluate the LP and sniping role as a package deal and apply probabilities to both roles instead of in isolation.

Misspecified Objective Function

Another issue is that sniped quotes are assumed to be losses by marking them relative to a future mid-price. This would be true for a pure LP/sniper; however, many HFTs can provide complementary services like implementing VWAP trading algos for large buy-side clients. A VWAP strategy does not simply cross the spread or jump on the best bid-offer, but employs both tactics when they find either attractive. It can include posting aggressive bids that are immediately taken or taking new aggressive bids as an alternative to merely crossing the spread. A resting order subject to HFT sniping leans on HFT liquidity; these other HFTs assist the LP in efficiently implementing their VWAP strategy.

An HFT is in a good position to sell $X of Apple stock at tomorrow's VWAP plus a fee that covers the expected trading fees, price impact, and spread. They profit if they can implement that strategy at a lower cost. Thus, a subset of an HFT's orders may target minimizing trading costs instead of making a profit. How much of an HFT's limit order trading involves this complementary tactic? Who knows, but the fact that Budish has offered no estimate or even mentioned it is a significantly omitted variable.

Sequential 100 ms Auctions are Complicated

As for the alternative, frequent batch auctions held every 100 ms, this is a solution only an academic could love. The current system works very well, as evidenced by the dramatic reduction in spreads and fees since electronic market making arose (no thanks to academics, except Christie and Schultz).

The novel gaming strategies created by this mechanism are not well specified. The model does not even consider the standard case where trades happen on large queues, which is most of the time. One could easily imagine an endgame like the California Electricity market debacle circa 2000-2001, where a poorly implemented auction market was gamed, revealed, and then everyone blamed 'the market.'

Could LPs keep tight markets across instruments and market centers if matching were queued and pulsed like a lighthouse?  All exchanges would have to become frequent batch auctions and have the auctions synchronized within 1 ms for the discrete-time auction model to work. The Solana blockchain, which tries to synchronize at a 100-fold higher latency, goes down frequently. On the world equity market, such failures would generate chaos.

The Randomizer Alternative

In BCS, they briefly address the alternative mechanism, adding randomized delay. They note it does not affect the race to the top. However, it affects the amount they should be willing to pay for speed. For example, if new orders added a delay of 0 to 100 ms, the benefits of shaving 3 ms off the route from Chicago to New York would be negligible, as it would increase one's chance of winning a latency race by a mere 1% as opposed to 100%, reducing the benefit 100-fold. In their own model, eliminating these investments directly lowers the spread. If one had to change CLOBs to reduce the allure of wasteful investments in speed, this would be a much simpler and safer approach.

Talk about Stale Data

The data driving his extrapolated costs are from 2005-2011 for the ES-SPY data and 2015 for the LSE. Strangely, his recent 2023 presentations at a16z and the NBER did not update the data. Remember your cell phone capabilities circa 2005-11? Currently, the major exchanges all generate multiple hardware timestamps and correctly sequence incoming orders within 5 nanoseconds. If he is confident that his mechanism can save the world $5B a year, getting data from the 2020s would seem obvious. While technology has improved significantly, so have the tactics. No one in this field thinks a strategy backtested on message data from before 2022 is relevant. This is clearly an academic idea.

Co-located Level 2 Tactics != Regional Arbitrage

The microsecond speed race in their LSE data differs significantly from the ES-SPY arbitrage game. Co-located servers involve a trivial expense and are a massive improvement in efficiency. With co-location, you can have hundreds of investors at precisely the same distance with a leveled plain field. Without co-location, the competition for closest access will be discrete and more subject to corruption; the playing field will not be leveled, their costs will be higher, and they will have to maintain their own little data center. The costs and tactics for co-location vs regional arbitrage are incomparable, and we should not encourage regulators to treat them the same way.

 

As mentioned, the nice thing about this proposal is that it is clear enough to highlight its flaws. Those who just want to add a stamp tax to fund all of college (or health care, etc.) don't even try to justify it with a model; they just know its costs would tax people in ways that most voters would not feel directly. Nonetheless, like cash-for-clunkers, this is not an economic policy that will do any good.