Intelligent design is fascinating because when biologists debate probabilities they often disagree by orders of magnitude. For example, Doug Axe looked at a Beta-Lactamase enzyme and estimated that the ratio of amino acid permutations that would fold correctly and break down ampicillin is one in 10^77. In contrast, evolutionists point to research that generates much larger likelihoods. Telomere discoverer and Nobelist Jack Szostak and Anthony Keefe estimated that the likelihood an 80-amino long protein can bind to inactivated ATP to be on the order of one in 10^12. Most estimates are around 1 in 10^50, but some are as low as one in a thousand.1
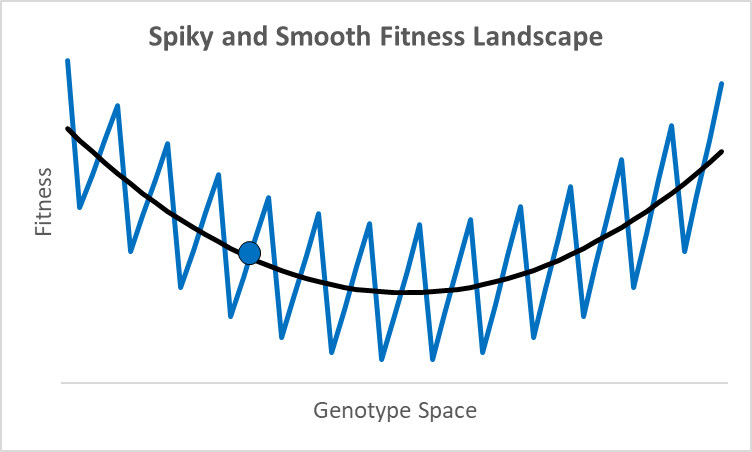
There are not many debates where scientists disagree by 77 orders of magnitude. While these researchers were looking at different proteins doing different things,2 they all thought their research was relevant to an essential question in evolutionary models: how smooth is the fitness landscape? To create new genes that created the original topoisomerase, or one of the 700 unique genes in both chimps and humans, it had to go from something—randomness, an existing or copied gene—to something new that aids fitness. Richard Dawkins portrays this as walking up a smooth hill behind what looks like an impenetrable cliff (Climbing Mount Improbable). This could be true, but not all peaks have smooth trails. For example, assume an organism is at the blue dot in the graph above, where the x-axis represents a one-dimensional fitness landscape while the y-axis represents fitness (the fitness landscape was popularized by Sewall Wright in the 1930s).
A century ago, a shift of allele frequencies in local populations was an adequate model for all evolutionary processes, as various allele combinations generate different phenotypes. However, with the discovery of DNA genes are more like computer code than a mixture of baking ingredients, and proteins have specific folds, alpha and beta sheets, and binding sites with distinctive 3-d shapes and polarity. In this context, moving up a fitness landscape could involve leaps across chasms where multiple specific amino acids are needed in particular locations to be viable or better. In this case, a hill-climbing algorithm could get stuck forever at a local maximum, like the 500-million-year-old nautilus with its pinhole-lens eye (its cephalopod cousin, the octopus, has a complex lens like a human).
My interest here pertains to a specific argument in Michael Behe's The Edge of Evolution, about the probability of generating multiple mutations that increase fitness. Behe noted the empirical likelihood of malaria developing chloroquine resistance is estimated at around 10^20, which was not disputed. The mutation rate of the malaria parasite P. falciparum is roughly 1 in 10^8 mutations per base pair per parasite. As there are 10^12 parasites in the human body on average, there are probably a thousand copies of every possible mutation to exist somewhere in each infected person. The resistance rate for atovaquone is 1 in 3 people, within an order of magnitude of what is expected. The probability of 10^20 suggests that malaria needs two mutations almost simultaneously, in that one alone is not common in the gene pool.
Evolutionists universally emphasized disagreement on this point (see Coyne, Miller, Moran). They argued that cumulative selection makes comparisons to monkeys typing Shakespeare, tornados assembling 747s in a junkyard, or two simultaneous mutations, all irrelevant. This assumption allows the belief that macroevolution is just microevolution over extended time frames. Notably, none of these critics proposed a model consistent with the 10^20 datapoint, whether the probability of n mutations scales at say, p/n vs. p^n.3 A couple of years after Behe's book was published, researchers documented that two mutations to the malarial PfCRT protein were necessary for chloroquine resistance. One mutation alone seemed deleterious as there were not many malaria with one of the needed mutations, ready to reach a new fitness level via the second one.
I found an excellent way to model this is using lattices. Lattices are helpful in option pricing, such as the binomial options model of Cox-Ross-Rubinstein. A barrier option model is analogous to the situation where a proto-protein needs n specific amino acids to gain some new functionality. This approach shows how if you need n specific mutations to get some higher fitness level, the cumulative probability of getting these will be observationally equivalent to the likelihood of getting these mutations sequentially.
The Model
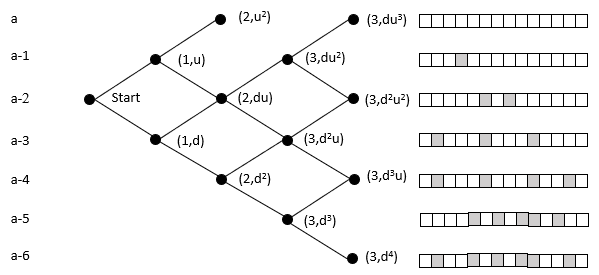
The probability of reaching a lattice node is the sum of the probability of all the paths to that node (Pascal's triangle). An organism moves rightward through the lattice with each mutation in its germ line. While this ignores heterozygosity, the point is to clarify the relative magnitudes of the cumulative vs. 'simultaneous' mutation; the refinement can be added later without loss of generalization.
The top row of nodes represents states where a descendant has a complete sequence of the targeted functional protein. We terminate the lattice at this point because the organism's germ line generates the functionality of interest. In the case of malaria, at this point, it can withstand the chloroquine and grow exponentially within the host, and break free to enter another host.
In the above example, the initial state is at the far left node. Here we model the case with 14 amino acids, and each level beneath the top row represents an increase in the number of amino acids needed to reach the target. It does not matter which amino acids are incorrect. For example, the initial state may need two specific mutations, but later on, the organism could be at a state where it requires two different mutations. These scenarios would have the same probability of reaching the target in this model.
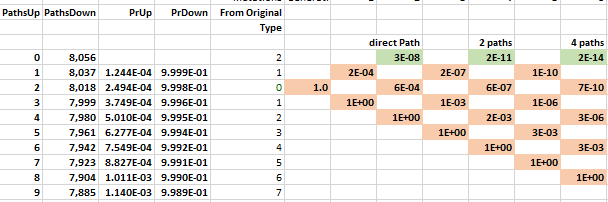
The probability of moving up is the same for all nodes on the same row in the lattice. The probability of getting 1 of 2 specific acids is the same regardless of which amino acids do not match and what the pathway was to get there. The probability of moving up, p(u), goes down as one moves upward because the number of possible good mutations relative to the number of possible bad mutations goes down. For example, if initially, we need two specific changes, and with 424 aminos that means there are 8056 (422 times 19 amino acids) ways to move away from the target, and two ways to move towards the target, creating a 0.025% probability (2/(422·19+2)) of moving towards the target. You can play with parameters in the excel sheet linked below.
It may be that many of the amino acids do not affect the functionality of the target protein. For example, one could argue that two specific mutations are needed, but only 212 of the other amino acids are necessary for functionality. In this case, we just change the number of total amino acids from the actual 424 to a 'functional' 212, as the others are irrelevant.
The mathematical intuition for this result is the following. The number of paths to the top row increases by a factor of 4 as one moves through time. In the chloroquine example, the top nodes represent all the combinations with two more up movements than down movements: up-up, up-down-up-up, etc. The probability of these successful paths declines by a factor of 0.001 because each path requires the extra p(u); a downward move implies an additional implausible upward move to get back to its earlier closeness to the target. The net probability--the number of paths times the probability, 4 × 0.001—therefore decreases by orders of magnitude at each step. Adding numbers that decline by an order of magnitude or more leaves the first digit unaffected, as when you add the numbers 0.01+0.0001+0.000001; the first term, 0.01, approximates the sum. In this way, the probability of a direct path number approximates the cumulative probability.
If we consider that mutations are like Poisson probabilities, happening randomly through time, the likelihood of two sequential specific mutations is equivalent to the probability of two simultaneous specific mutations. The direct sequence of mutations is precisely like the probability of a simultaneous mutation.
In the infinite limit, the odds of reaching the target are 1.0 regardless of how close one is to a target. The standard way of modeling probabilities ignores the pathways and looks at limits, obscuring this result.
While many paths lead to the target, as a practical matter, they are irrelevant. One can imagine all sorts of intermediate configurations of amino acids that are useful for something else, but that is not science unless one has a reasonable model or an empirical estimate of the ratio of these viable configurations to those possible. We all know that to turn a bicycle into a motorcycle you need several parts to work together. One can imagine each part being added without customers noticing, but one can also imagine a point where the thing does not work at all. To change an ion channel from one that lets only sodium across a membrane to one that allows only potassium, it too needs many specific mutations before it would work at either task. It could be there are many intermediate configurations that do something entirely different, but without any actual data, it takes a lot of faith to imagine these unseen functional intermediates are all buried in our past.
This process helps understand why looking at evolution in real-time on fruit flies, and E. coli shows nothing that would extrapolate to novel functionality. Instead, the more common involves loss of function. For example, losing melanin is advantageous for humans in northern latitudes because it allows humans to get more vitamin D. At the same time, the risk of skin cancer is lower with less sunlight, so the benefit of melanin is less. The sort of evolution we see all over within families like cats, dogs, and bears, however, does not explain how we got cats, dogs, and bears from a common ancestor.
Reidhaar-Olson and Sauer 1990 mutated the lambda-repressor in E. coli and found that only one in 10^63 sequences yield a functional repressor fold. Yockey 1977 calculated that the likelihood of generating a functional cytochrome c sequence is one in 10^65.
Axe checked how many amino sequences would have stable functional folds and maintain beta-lactamase enzyme activity. Szostak looked for proteins that bind to ATP, the largest family of all proteins. Most ligands bind to a single protein fold (83%), while the ATP binding binds to 35 different protein folds
The ignorance and indifference to probabilities among evolutionists are astounding. For a long time, many would just mention hundreds of millions of years and assume anything could happen. Most famously, in the Huxley-Wilberforce debate a mere year after Darwin published Origin of Species, Huxley suggested that a bunch of monkeys could produce the 23rd Psalm given enough time. The implication is that virtually anything is possible given enough time. The probability of typing Hamlet alone is around 10^184000, excluding punctuation. 500 million years would not give us the 23rd Psalm even if every bacteria were a monkey typing every second since the beginning of the universe.
This ignorance was highlighted when a researcher suggested that completely random mutations created a new protein in bacteria that degrades nylon. This assertion came from a misunderstanding popularized by professor of biology William Thwaites in 1985, who claimed that the enzymatic activity arose from a frameshift mutation within the bacteria that created an entirely novel sequence of amino acids. Such a mutation would shift every codon over one, creating an entirely new set of amino acids, like how changing one character affects a SHA-256 hash output.
It turned out the bacteria could already digest nylon, but the substitution of just two amino acids gave it a 153-fold increase in activity by widening a linkage cleft. While neat, that’s nothing like creating, say, topoisomerase or a ribosome. What’s interesting to me is that biologists could imagine that a random sequence of 392 amino acids would be functional. Clearly, professional biologists have a very different intuition on the probability of creating a new functional protein.
No comments:
Post a Comment