Recently deceased philosopher Daniel Dennett called Darwin's idea of natural selection the best idea anyone ever had, a universal solvent that melts away all the problems in biology. Dennet had contempt for Christians, coined the term 'brights' for those who shared his worldview, and thought it wise not to respect religion because of its damage to the 'epistemological fabric of society.' Like fellow atheist Richard Dawkins, he never debated biologists, just theologians.
In a 2009 debate, Dennet mentioned he brought his friend, an evolutionary biologist, to a 1997 debate with Michael Behe about his book Darwin's Black Box (1996) because he felt unqualified to address the micro-biology arguments. Dennett described Behe's book as 'hugely disingenuous propaganda, full of telling omissions and misrepresentations,' that was 'neither serious nor quantitative.' Dennet then added he would not waste time evaluating Behe's newest book, The Edge of Evolution (2007).1
Dennett emphasized his approach to understanding the world was rational, reasoned, and evidence-based. Yet, he never directly addressed Behe's arguments and instead stuck to the cowardly pleasure of debating non-scientist theologians with whom he had greater knowledge of biology. He admits he could not evaluate the arguments alone by enlisting a biologist to help him debate Behe. If he could not trust himself to evaluate Behe's argument, a rational approach would be to take a trusted source's opinion as a Bayesian prior, not as a fact so certain that its negation damages the epistemic fabric of society. Unfortunately, many, perhaps most scientists, agree with Dennett and think the only people who don’t believe in evolution are ignorant (e.g., see Geoffrey Miller here, or Dawkins here).
If Dennett had read Behe's Edge of Evolution, he would have seen it as a logical extension of his earlier book, not moving the goalposts. Behe's argument isn't based on parochial microbiology knowledge; it's pretty simple once one gets the gist.
Behe highlighted the edge of evolutionary power using data on malarial resistance to two different antibiotics. For the malaria antibiotic atovaquone, resistance develops spontaneously in every third patient, which, given the number of malaria in a single person, the probability malaria successfully adapts to this threat can be estimated as one in 1e12, or 1e-12. Resistance occurs once every billionth patient for the antibiotic chloroquine, giving an estimated successful mutation probability of 1e-20. This roughly squares the original probability, which led Behe to suggest that at least two mutations were required to develop resistance, as two mutations represent a squaring of the initial probability. This prediction was confirmed a few years later.
Extending this logic, given a base mutation rate of p per base pair per generation (e.g., p ~1e-8 for humans), if n mutations are needed, the probability of that happening scales at pn. Given that new proteins require at least 10 changes to some ancestor (out of an average of 300 aminos), the probability of an existing genome evolving to a new specific protein would be 1e-80. Given that only 1e40 organisms have lived on Earth, this implies that evolution is limited in what it can do (note most evolution we observe, as in dog breeds, just involves changes in allele frequencies).
A reasonable criticism is that this argument works for a specific target, such as Behe's example of malaria overcoming an antibiotic. However, the state space of possible unknown proteins is much larger. For example, the average protein has 350 amino acids; with 20 amino acids, that's 20^350 or 1e455 possible permutations. If there are islands of functional proteins within this vast state space, say at only a rate of 1e-55, that leaves 1e400 potential targets. The 'singular target' criticism does not invalidate Behe's assertion, but addressing it would require too much space for this post, so I will just mention it as a defensible criticism.
However, most reviews of Behe's malaria-based argument centered on the simple assertion that generating n specific mutations scales at pn.
Ken Miller (Nature, 2007):
Behe obtains his probabilities by considering each mutation as an independent event
Sean Carroll (Nature, 2007)
Behe's chief error is minimizing the power of natural selection to act cumulatively.
Jerry Coyne (The New Republic, 2007)
If it looks impossible, this is only because of Behe's bizarre and unrealistic assumption that for a protein-protein interaction to evolve, all mutations must occur simultaneously, because the step-by-step path is not adaptive.
These criticisms are based on two possible assumptions. One is that if multiple mutations are needed, single mutations encountered along the process of fixing the multiple mutations may each confer a fitness advantage, allowing selection to fix the intermediate cases. While this can be true, it is not for the mutations needed for malaria to develop chloroquine resistance, which needs at least two, and it is undoubtedly not true in general. Indeed, a good fraction of the intermediate steps reduce fitness, some severely (see here or here), which is why a fitness advantage from a two-step mutation does not happen with the same frequency as fitness enhancement that needs one mutation: in the wild, the intermediate mutations are eliminated from the population.
The other assumption would be if the number of indirect paths overwhelms the specific case where sequential mutations occur. There are many indirect paths from one sequence of 300 amino acids into another. The question is their probability, the sum of these successful paths over all possible paths.
Intuitively, multiple specific simultaneous mutations are astronomically improbable and would constitute an impenetrable fitness valley, which is why evolution proponents are emphatic that it is an absurd approximation. Their intuition is that if one needs a handful of specific mutations when one already has 100 or 400 of the needed amino acids in the correct spot, a cumulative process of some sort should be likely, even if the final steps involve neutral mutations that neither help nor hurt fitness. However, none of Behe's critics generated a model to quantify their reasoning, even though they are all scientists in this field.
Model of the Behe Edge of Evolution Argument
Hypothesis: Prob(get n specific mutations sequentially) ~= Prob(get n specific mutations over 1e40 generations)
The model below uses a trinomial lattice to show that if the probability of getting one mutation correct is p, the probability of getting n mutations correct is on the order of pn. Given the small probability of getting one mutation correct, this highlights what Michael Behe calls the edge of evolution: the fitness landscape generates an impenetrable barrier for naturalistic processes. Assuming simultaneous mutations towards the target captures most of the cumulative probability of reaching that target if mutations are neutral until the target is achieved. The other paths drift away at a rate that initially eliminates the benefit of being so close.
We can model this using a variant of Richard Dawkin's Weasel program that he used to demonstrate the power of evolution. It starts with a string of letters and spaces, 27 potential characters in a string of length 28.
neuh utnaswqvzwzsththeouanbm
Dawkins randomly generated strings, fixing characters that matched the target phrase from a Shakespearean play. The application to genetics is straightforward if we think of the phrase as a sequence of nucleotides or amino acids creating a protein.
…
xethinks dt is like a weasek
xethinks dt is like a weasel
xethinks it is like a weasel
methinks it is like a weasel
This algorithm fixes the characters that only make sense at completion. This is like assuming necessary mutations are selected with foresight, which would require some outside designer shepherding the process. Evolutionists countered that Dawkins' weasel program was merely to demonstrate the difference between cumulative selection and single-step selection, but this is disingenuous, as removing forward-looking selection increases the number of steps needed from 100 to 1e39, which would not make for a convincing TV demonstration (see Dawkins’ promoting his weasel here).
Nonetheless, the Weasel program is familiar to many who study evolution and can be used to illustrate my point. Consider the case where we are two characters away from the target sequence.
Start: 2 wrong, 26 correct
XXTHINKS IT IS LIKE A WEASEL
Case 1, closer: 1 wrong, 27 correct.
MXTHINKS IT IS LIKE A WEASEL
XETHINKS IT IS LIKE A WEASEL
Case 2, stasis: 2 wrong, 26 correct. The two mismatched characters can each change into 25 potential targets (27 – 2) that are also wrong, for a total of 2*25. For example, here are three.
YXTHINKS IT IS LIKE A WEASEL
XYTHINKS IT IS LIKE A WEASEL
AXTHINKS IT IS LIKE A WEASEL
Case 3, further: 3 wrong, 25 correct. Each of the remaining matching characters can become unmatched by changing into any of the 27-1 potential characters. The total number of paths is 26 x 26. Here are two.
XXXHINKS IT IS LIKE A WEASEL
XBTHXNKS IT IS LIKE A WEASEL
To generalize the problem, let us define L as the string length, c the number of potential characters at each element in the string, and n the number of needed changes to the string (initial mismatches). The set of potential new strings can be split into three groupings with their distinctive number of paths:
1. strings that have more characters that match the target:
a. e.g., n moving from 3 to 2, n possibilities
2. strings that have the same number of characters matching the target: n*(c – 2) possibilities
a. e.g., n changing one mismatched amino to another, so staying at 3
3. strings that have fewer characters that match the target: (L – n)*(c-1) possibilities
a. e.g., n moving from 3 to 4
The probabilities are the same regardless of which n characters are referenced. For example, the two sequences below are mathematically identical regarding how many paths are towards and away from the target, so they will have the same probabilities of moving towards or away from the target.
XXTHINKS IT IS LIKE A WEASEL = METHINKS IT IS XIKE A WEASLX
This makes the problem simple to model because regardless of where the string starts, the number of cases that need probabilities is at most L+1, as n can range from 0 to L. All mutations are considered equal probability; the number of paths up over the total possible paths {up, same, down} is the probability of moving up. We can, therefore, calculate the probability of moving closer, the same, or further from its target (i.e., nt+1 < nt, nt+1 = nt, nt+1 > nt) for each n <= L. This allows us to model the evolution of the string using a recombining lattice that evolves from an initial node, a standard tool for modeling option values.
At every row of the L+1 nodes in the lattice, we calculate the probabilities of moving up, across, and down via the following formulas.
1. Prob(closer): n/(L*(c-1))
2. Prob(same): n*(c-2)/(L*(c-1))
3. Prob(farther: (L-n)*(c-1) /(L*(c-1))
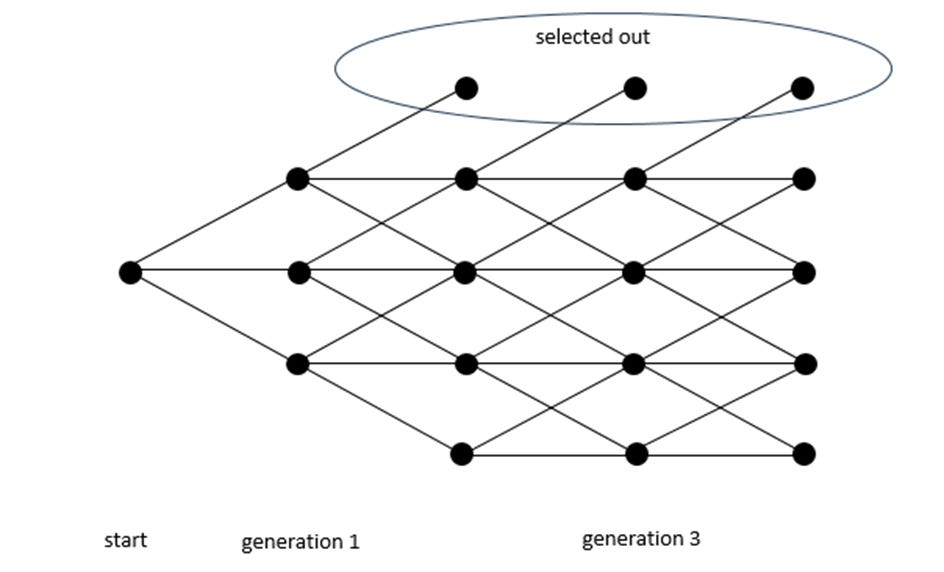
Figure 1 below shows a case with five rows representing a string of 4 characters. The columns represent generations defined by a change in one of the spaces in the sequence (a mutation). The bottom row of nodes reflects zero matches, and the top level is a complete match. In this case, the initial node on the left implies 2 mismatches out of 4. If the new mutation flips a mismatched position to the target, it is closer to the target and thus moves up one level, just below the top row; if it stays two away by having an incorrect letter changed to a different incorrect letter, it moves horizontally; if a correct letter changes to an incorrect letter, it moves down.
Figure 1
A complete match is a success, and we assume that once the sequence reaches the target, it does not regress (it is then subject to selection and fixates in the population). Thus, there is no path downward from the top row. While this is not realistic in practice, it inflates the total probability of reaching the target and does not affect the gist of my argument. The point is to highlight the relative importance of the direct path as opposed to the actual probability.
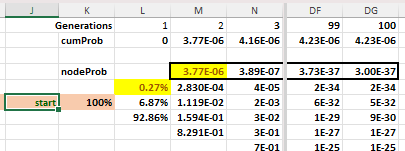
In Figure 2 below, we have a snip from a worksheet modeling the case where the starting string has two mismatched characters from the target sequence of 'methinks...' For the first mutation, there are 676 changes away from our target, 50 that would maintain the same distance, and 2 that move towards the target, giving probabilities of 92.8%, 6.9%, and 0.3% to the node branches. At the next upward node in step 1, the probability of going up again and reaching the target is 1/728 or 0.14%, so the probability of reaching the target in two mutations is 0.27% * 0.14%, or 3.77e-6.
Figure 2
The 'nodeProb' row represents the probability of reaching the target on that mutation, while the 'cum prob' row represents the cumulative sum of those nodes, given we assume reaching the target allows the organism to thrive with its new protein function.
The node probabilities asymptotically decline, so taking the hundredth 'nodeProb' as equal to all subsequent nodeProbs generates a conservative estimate of the number of generations (G) needed to double the direct path probability.
2*nodeProb(2) = cumProb(100) + G*nodeProb(100)
G = (2*nodeProb(2) - cumProb(100) )/nodeProb(100)
For this example
G = (2*3.77e-6 – 4.23e-6)/3.00e-37 = 1e31
This implies at least 1e31 generations are needed for the cumulative probability to be twice the direct probability. As estimates in this field have logarithmic standard errors (e.g., 1e-10 to 1e-11, as opposed to 1.0e-10 to 1.1e-10), a direct path probability within a factor of 2 of the cumulative case over 1e31 paths is about the same.
Modeling this with a lattice allows us to see the relative importance of the direct path because everything reaches the target over an infinite amount of time, so the probability of reaching the target is the same regardless of the starting point. With a lattice approach, we can model the finite case that is still large enough (e.g., 1e40) and see the relative probabilities.
The probability of a direct path is approximately equal to a simultaneous path because, if we assume mutations obey a Poisson process, the probability of a simultaneous mutation is the same as sequential mutations, just one probability times the other. For example, the malarial parasite cycles through several generations during an infection, and the resistant parasite could acquire the necessary mutations in generations 3 and 5 or simultaneously in generation 3 (both would have the same probability).
Thus, Behe's hypothesis that the probability of reaching a target n mutations away scales with pn is a reasonable estimate when intermediate steps are neutral.
The worksheet contains the Weasel program applied to 2 and 3 characters away from the target. It can be generalized straightforwardly for an arbitrary n of needed mutations, 20 amino acids, and protein of length L, as shown in the worksheet ‘12awayAminos.’ Looking at the worksheet '2away' in the Excel workbook, the probability of reaching the target in a direct sequence is the probability of hitting the first top node. All the probabilities here are relative because this model assumes a mutation along an existing string of amino acids. This occurs only at a rate of 1e-8 per nucleotide per generation in humans. So, the extension to amino acid changes needs an extra adjustment (nucleotide changes do not necessarily change amino acids). The purpose of this post is just to show the relative probability of the direct and indirect paths, which is independent of the absolute probability.
There are an estimated 35 million single nucleotide differences and 90 Mb of insertions and deletions, creating 700 new genes in chimps and humans that were not present in our last common ancestor. That's at least 100 functional mutations that must be fixed every generation over the past 6 million years. Genetic drift can generate the 100 newly fixed mutations, but this drift is random. The probability that a random amino acid sequence would do something helpful is astronomically improbable (estimates range from 1e-11 to 1e-77, a range that highlights the bizarre nature of evolution debates), which creates a rift within the evolution community between those who emphasize drift vs. those who emphasize natural selection.2 This debate highlights that there are rational reasons to reject both; each side thinks the other side’s mechanism cannot work, and I agree.
In Dawkin's Mount Improbable, he admits the de novo case is effectively impossible. He suggests indirect paths involving gene duplication, as the base structure provided by an existing gene would give the scaffolding needed for protein stability. Then, one must merely nuance a few segments to some unknown function. The above shows that if one needs a modest number of specific amino acids (e.g., a dozen), the probability of reaching such a target will be greater than 1 in 1e100. For this copy-and-refine process to work, it requires a protein space with a dense set of targets—islands of functionality in the protein state space—which is possible but eminently debatable.
See the 2009 debate between Dennett and Christian philosopher Alvin Plantinga, especially around 64 minutes in.
The 1e-11 estimate applies to an 80-amino string converting from weak to strongly binding to ATP, which is understandable given this is the most common binding protein machine in a cell, as it powers everything. Further, this was studied in vitro, which is 1e10 less likely to work in vivo. The 1e-77 estimate is for beta-lactamase, an enzyme produced in bacteria with a specific function, unlike binding to ATP which is common. Other estimates include 1e-65 for cytochrome c, 1e-63 for the bacteriophage lambda repressor, and 1e-70 for a certain phage protein.
No comments:
Post a Comment