 |
Panoptic promotes a vision where users can create virtually any standard combination of puts and calls on the blockchain without an oracle, auction, or limit order books. This would be very useful because options are difficult for market makers because of their convexity and leverage. An option's lambda captures leverage:
Lambda = option%change/underlying%change
A lambda of 10 implies a 1% price change generates a 10% option price change. Option lambdas range from 2 to 100 depending on volatility, maturity, etc., but generally are around five to 15. This is one of the primary reasons options are popular: option buyers can get 10x leverage without worrying about margin. Options often expire worthless, so they aren't less risky than leverage, but removing the liquidation scenario simplifies it.
With only leverage, this would not be a problem for market makers, as it would just be the difference between a market maker trading 10x more size than another. However, options generally have a high convexity, as measured by its gamma.
Gamma = change in delta/change in underlying price
With the delta changing, market makers are not just trading an asset 10x the size of its underlying but must hedge this convexity, which is costly. This volatility increases the spread on options relative to stocks due to the gamma alone. The three orders of magnitude greater latency in the blockchain exposes option market makers to insurmountable adverse selection.
My favorite solution would be to create an option contract that traded on the implied volatility, not the price. As one wag once said, “Implied volatility is the wrong volatility in the wrong model to get the right price.” All Black-Scholes inadequacies can be rectified via a suitable skew adjustment to the implied volatilities for various maturities and moneyness. Implied vols fluctuate much less than the price, generating an order of magnitude less option price volatility than actual option prices. One could trade on implied vol and then use a forward-starting underlying price, such as the price read from a liquid AMM's contract, and apply the Black-Scholes model to calculate the price. I used to work for an options market maker, and implied vols are how traders intuit prices anyway, as multiple rolling maturities and strikes make option prices an afterthought.
A New Way?
The basic stochastic process used in financial derivative theory started in biology. In 1827, Robert Brown described the path of pollen grains moving in water in what was to be called Brownian motion, the forerunner of the random walk applied to stock prices. Thus, it makes sense that Guillaume Lambert, a Cornell biophysicist, was well-equipped to analyze option-like properties of constant product automated market makers like Uniswap. After writing a few pieces and getting a Uniswap grant, he eventually secured funding to start Panoptic, a protocol for buying and selling option positions based on AMM liquidity provider (LP) positions.
His fundamental insight is that since Uniswapv3 LP positions have negative gamma, with ranges defined very granularly (every ten basis points), one can use these as the base for replicating any option. The basic idea comes from the Black-Scholes partial differential equation, which shows that an option premium equals the expected convexity cost, the expected value over all expected price paths, covering different gammas and stock prices.
If the option seller delta hedges continuously, his cost will be based on a similar function, the only difference being that volatility will potentially change over time (this was rebranded as loss versus rebalancing, but it's the same thing).
Thus, the PnL for the hedged seller is just the difference between the realized and implied variances. In equilibrium this is zero, implying the expected convexity costs (hedged or unhedged) equals the option premium.
If a Uniswap pool is priced so LPs have a zero PnL, or perhaps some equilibrium gamma risk premium, the fees generated for each range equal their expected dollar gamma. One then just uses various ranges to create arbitrary option payouts, and the realized fee revenue will generate the requisite option premium for the realized gamma. This differs from standard options, where a buyer pays the option premium upfront.
Thus, Panoptic presents the standard out-of-the-money LP position as a covered call, which seemingly can be captured via a liquidity range within an AMM pool.
At 30k feet, the ability to create options like those above seems plausible. The problem is that the options within an AMM LP position are a set of micro-straddles the seller can exercise at any time. For any one block, the option is only active in a small range, 0.1% wide. Outside this range, the LP’s options generate no fees and incur no convexity costs.
For example, consider the following range covering 104 to 106 (the same logic would apply to a range of 0.1%). This shows the standard covered call or short put nature of LP positions, in that if the current price is 108 to the right, the LP position is short a put; if the current price is to the left at 100, the LP position is effectively in a covered call position.
What makes this weird is the gamma for these ranges is zero outside their range.
Up to the lower range bound, the seller of this option (the LP) gets no option decay premium; gamma is zero, and so is the fee revenue.
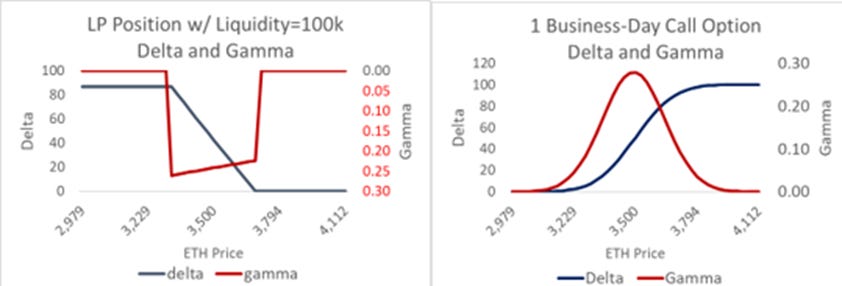
As a practical matter, this means arbitraging an LP using listed options would be a nightmare. Consider this LP range and a 1-business-day option with a similar gamma.
The smooth Gaussian distribution to the standard option, even with a 1-day maturity, is a poor fit. See the net delta and gamma below.
The spiked changes in delta and gamma at the end of this +/-5% range imply that standard options will not help hedge one's LP position, and it would be better to simply delta hedge the LP position. This highlights how the LP position looks like a standard option only from far away. When the LP position is out of the money, it is not option-like; when it is active, the shortest-dated options traded on Deribit will be informative but otherwise useless.
Out-of-the-money Option as a Synthetic Put/Call Dynamic Strategy
Standard Put Option
While it's easy to generate a graph showing how an LP position is like an out-of-the-money put or call, a better analog is a synthetic version of these options. This is because a standard option has a positive value at the start, paid by the buyer to the seller, which does not apply to LP ranges. For example, if the current price is $3500, a put can be calculated using a simple lattice for the future value of an asset and its corresponding asset prices.
Long Stock with Put
Expected Value = $3,559
Minimum Value = $3,500
Option cost $59
Without the put option, the expected price is $3500 (multiply final prices with final probabilities and add them up). The put option replaces the bottom price with the strike price of $3500. When multiplied by their various probabilities, the expected value is now $3559, implying the put value of $59. A buyer can pay $59 to raise his worst-case scenario from $3274 to $3500. These two scenarios have the same expected value, and some find the option scenario preferable.
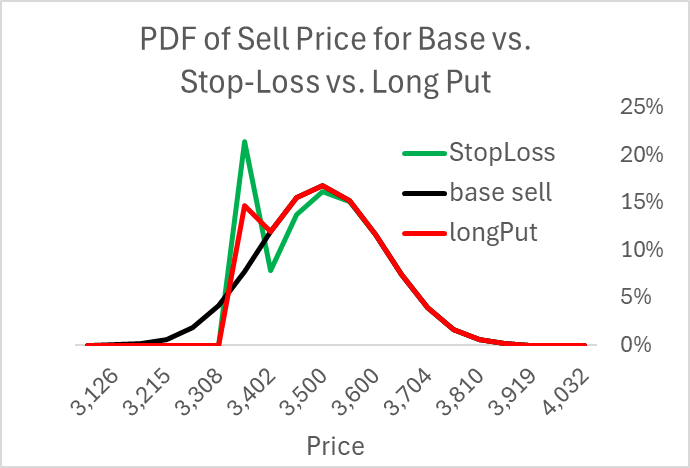
Stop-Loss Strategy
Now, consider the stop-loss strategy. Here, one owns an asset at $3500 but instead of paying for a put option, he adopts the dynamic strategy to sell it when the price falls. This also raises the price in the worst-case scenario, but here, the expected value of the asset is the same, $3500, and there is no upfront cost.
Stop-Loss Strategy
Expected Value = $3500
Minimum Value = $3385
Another way to see this is to note that with the stop-loss, while one can raise the minimum stock sale price up to the strike, the cost comes from missing out on those times when the price rebounds. The expected value of all these scenarios is the same (once one includes the cost of the put option).
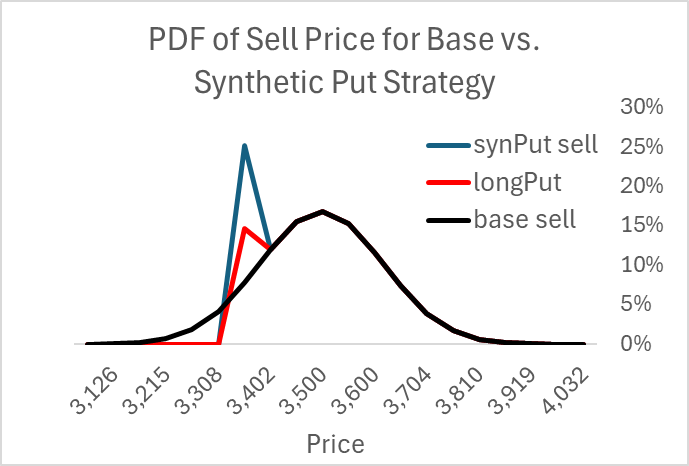
Put Replication Strategy
A better analog to the Panoptic put option is a replication strategy that sells when the price falls below a certain level and then repurchases it if it goes back above. This enables the owner to capture more of the upside. An out-of-the-money range is like a synthetic option replication strategy in that it generates no cost or revenue when not touched.
Consider the trinomial lattice shown below. With a trinomial lattice, the price moves up, down, or stays the same (roughly ¼ for up and down, ½ for staying the same). The price starts at $3500, and each period experiences a 1% volatility. He sells when the price falls below $3400, and when it rises above $3400, he repurchases it. Thus, in the first green cell with 6.3%, in the next period 1.6% chance the price will fall below $3400, and a sale will occur. In the period just to its right, in period 4, we do not assume 3.2% of these cases will sell, only those that are moving downward, so that would be about 2.4% (~0.25*0.095). Similarly, we estimate the buy-backs using only those probabilities below $3402 that rise in the next period. So, in period 7, we have about 3.1% of that period buying at $3402 (0.325*0.055).
The result is to better match the put option regarding the sale price. As with the put option, the sales-price PDF dominates the base case.
Of course, I'm missing something because the put raised the expected sale price but cost money. Here, the synthetic put cost nothing but a bit of work. The cost comes from the extra trades reflected in the fact that the synthetic put's PDF is much higher than the other two distributions. This extra selling comes from extra buying. Every buy before the final period represents an extra round-trip trade compared to if we just ignored the price until the end.
In those extra transactions we sell low ($3355) and buy high ($3402), a loss. Unsurprising, the net cost of these trades exactly equals the cost of the put. This is an excellent way to intuit the earlier assertion that the expected convexity costs of a continuously delta-hedged option equals the option premium,
Out-of-the-money (OTM) puts and calls would provide users with an attractive strategy for implementing this strategy, removing the need to place all those orders as in a dynamic strategy. The problem is that I don't see anyone wanting to sell them.
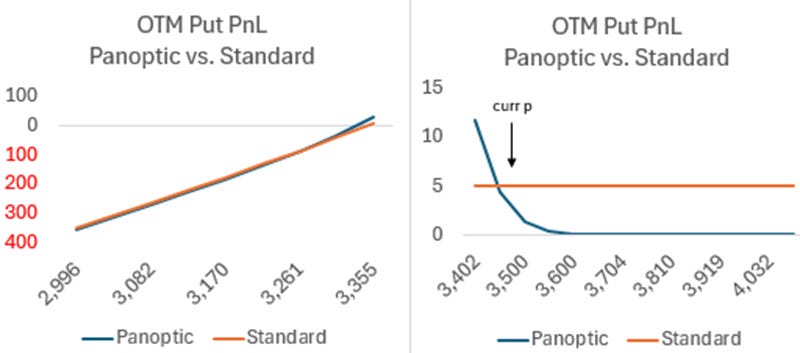
Unattractive Short Out-of-the-Money Put PnL
For the foreseeable future, one will not arbitrage volatility selling an LP position against another, as that requires low spreads. It took decades for that sort of liquidity to build up in tradFi, and we are not close. Even today in tradFi, those who arbitrage relative vol between two assets are almost always professionals with the lowest fees, capital requirements, and fastest trading platforms. Retail option traders generally have a view about the future price, not implied option movements, because they do not have the low-cost access that would make trading this profitable.
The OTM option sellers on Panoptic will see an unfamiliar payoff. Consider the retail tradFi payoff
Revenue: option premium (expected convexity cost)
Retail Cost: Max(strike – price, 0)
In Panoptic, assuming the AMM is priced at cost, we have
Revenue: realized fees (realized convexity costs)
Retail Cost: Max(strike – price, 0)
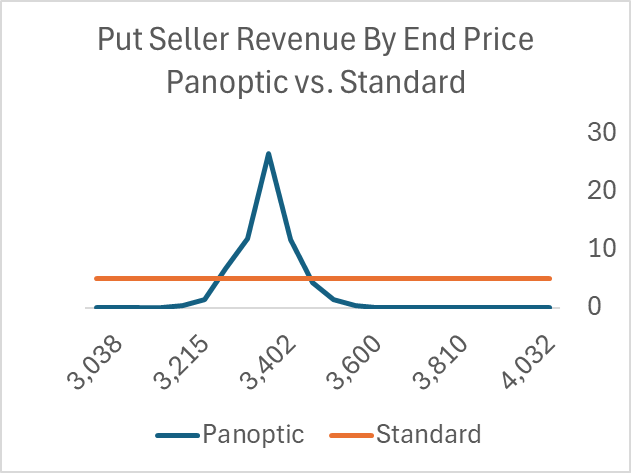
For Panoptic the revenue switches from expected to realized convexity (which, if priced correctly, shows up in LP fees). This dramatically changes the payoffs for the OTM option seller. For the happy case where the price rises, the payoff for the standard OTM put seller gets his option premium as pure profit. The Panoptic put seller, however, gets nothing unless the price ends close to his strike. For the unhappy case where the price goes down, the scenario is similar. [I had to break these two cases into different graphs because the downside pnl is so much larger.]
I don't think retail put sellers will find this payoff attractive. The Panoptic put seller will be betting that the price will not go much below or above their strike, while a standard retail put seller thinks the price will increase. This is because in Panoptic the seller's revenue looks like the graph below, quite different than what one sees in a standard option.
Panoptic's OTM put is more like an out-of-the-money straddle. That's a unicorn in retail option strategy because no one wants it.
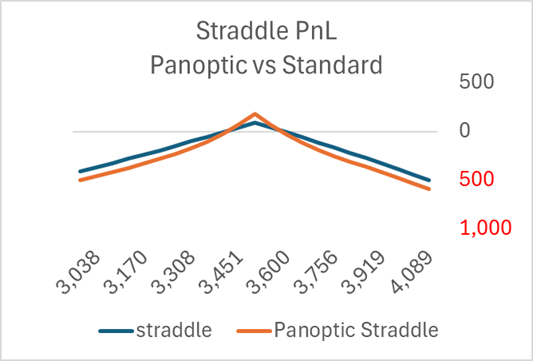
In contrast, the standard at-the-money straddle is potentially attractive, as the differences are relatively minor between the Panoptic and standard option PnL.
More Problems
Several unwelcome features remind me of another Uniswap-promoted complementary product, Squeeths. This product was sold as a way to hedge LP risk by allowing people to go long perpetual gamma, the opposite of what is generated by the LP position (short perpetual gamma). It traded on the price of the underlying squared, such as squared eth.
However, to match an LP position’s gamma, the squeeth requires at least ten times the delta, which must be hedged elsewhere. The capital required would explode. A good hedge reduces required capital.1 Another terrible thing about squeeths is they are not like buying a variance swap, which is like a futures contract on variance. Instead, they are a sequence of forward-starting one-day variance swaps, meaning, if you thought volatility was cheap, by the next day, it would be repriced, so subsequent days are all afresh. Going long a squeeth was like a position on the future daily conditional expected variance over the realized variance, something not seen off the blockchain because no one wants it.
[I just checked the squeeth team's Twitter, and they are hiring developers, highlighting no one cares whether something has or will work, just that it’s plausible. I used to think squeeths were the worst idea I have ever seen on the blockchain, but that's reserved for in-game leveraged sports betting (the creators thought the standard 5% vig would magically disappear in-game). As if a bet where the payoff is +100 or 0 needs leverage.]
Similar to squeeths, Panoptic positions have some unattractive practical aspects (though, not that bad). For example, there does not seem to be a reason to use actual LP positions. These are created when the option seller mints the option, but if a buyer arrives, they are instantly exited. One could simply read the GlobalFee and liquidity for the relevant ticks off the Uniswap contract, get the requisite information, and avoid wasteful expense.
Then, there is the cost of a seller canceling. As the essence of an LP position is that the option seller can costlessly exit each block, this is a significant change to the base short gamma position. TradFi options require a premium because people must be paid for locking them in over time, as only the buyer can exercise early. Daily options are popular but they too require a payment, so it's not like demanding the sellers don't revoke their straddles for only a few days is irrelevant.
Lastly, the option seller pays a commission. Considering LPs usually lose money, I don't think anyone will find selling options using LP positions as a base would make it an attractive stand-alone investment. The best targets are current LPs. One could give them the option to take their LP positions, and buyers would promise to give them the same payout, with an extra 5% or 10% on the fees. This would be easy to do, and the option sellers would be better off without cost or risk. Buyers could get long volatility without the vega premium one sees in tradFi, which could work.
Strangely, Guillaume occasionally mentions the low implied volatilities for Uniswap pools but has never documented this thoroughly. I would think showing how one can pay LPs 10% more and get access to long vega without paying the tradFi vega risk premium would be an excellent selling pitch. He could present various back-tests showing exactly how to make money or hedge volatility. Few people in defi—VCs, developers, or protocol CEOs—know much about the profitability of the most popular defi contracts, let alone how to take advantage of that.
I'm unsure what motivates this willful blindness to the actual profitability of the most active Defi contract. One cannot fix a problem that is considered taboo. I speculate that the lottery returns to prior projects that ultimately became zombies taught investors in this space to focus on the short term. Create something that looks like it implements something popular off the blockchain, note how it will be decentralized, etc., and ignore the details (eg, Augur). When everyone figures out the project is not viable, the insiders are all rich, and they move on to fund similar projects. Many faux-decentralized L2s and protocols exemplify this strategy.
Note that for an active LP position, we have
LP delta = liquidity / sqrt(p)
LP gamma = liq / (2*p^1.5)
the delta/gamma is 200, regardless of range width
In contrast, for squeeths
Squeeth delta: 2*p
Squeeth gamma: 2
Given ETH price of $3000, that's a delta/gamma of 3000
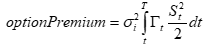
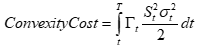
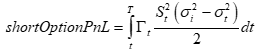







No comments:
Post a Comment