Generally, markets are efficient in that it isn't easy to make above-average returns day-trading, and most mutual funds underperform market-weighted ETFs. Yet historically, in various applications, options have been underpriced for decades. For example, asset return distributions were known to have fatter tails than the lognormal distribution back in the 1960s (see Benoit Mandelbrot ('62) or Eugene Fama (' 65)). Most option market makers, however, applied the basic Black-Scholes with a single volatility parameter, which underpriced out-of-the-money options. On a single day, October 19, 1987, the stock market fell 17%, which, using a Garch volatility estimate, was a 7.9 stdev event. From a Bayesian perspective, that did not imply a miracle but, rather, a misspecified model. Option market-makers soon adjusted their models for out-of-the-money puts and calls, ending decades of underpricing (20 years before NN Taleb's Black Swan introduced the concept of fat tails to the masses as if it were 1986).
Another example is convertible bonds, which are regular bonds that are convertible into stock at a fixed price, a bond plus an equity call option. The optionality was underpriced for decades. In the 1990s, a hedge fund that merely bought these bonds hedged the option's equity delta and bond duration and generated 2.0 Sharpes, which is exceptional for a zero-beta strategy. Eventually, in the early 2000s, investment bankers broke these up into bonds and options, allowing them to be priced separately. This isolation highlighted the option underpricing, and this market inefficiency went away. One could add Korean FX options that were underpriced in the 90s, and I'm sure there were many other cases.
So, there is precedent for a lot of money locked up in money-losing short convexity positions, as with liquidity providers (LPs) on automatic maker makers (AMMs). However, LP losses explain why AMM volume is still below its 2021 peak; transformative technologies do not stagnate for three years early in their existence unless something is really wrong. It's like how multi-level marketing scams like Amway have a viable business model relying on a steady stream of new dupes; they can persist, but it's not a growth industry.
The Target
The way to eliminate AMM LP convexity costs centers on this formula:
Impermanent Loss (IL) = LPvalue(pt) – HODL(pt)
LPvalue(pt) is the value of the LP position at the new price, pt, and the 'hold on for dear life' (HODL) portfolio is the initial deposit of LP tokens valued at the new price. It turns out that this difference is not an arbitrary comparison but instead captures a fundamental aspect of the LP position, the cost of negative convexity in the LP position. The expected value of the IL is the LP's convexity cost, which is called theta decay in option markets.
The LP convexity cost also equals the expected value decay of a perfectly hedged LP position (minus fees). Hedging is often thought of as reducing IL, and it does reduce the variance of the IL, eliminating extreme LP losses. However, this does not affect the mean IL, which, over time, equals the expected value. Lowering a cost's variance reduces required capital, which is why hedging is a good thing, but it will not solve the IL’s main problem, its mean, which is generally larger than fees for significant capital-efficient pools.
If we expand the above formula, we can rearrange variables to get the following identical equation as a function of pool token quantity changes and the current price (see here for a derivation).
IL = USDchange + pt×ETHchange
I am using a stablecoin USD and the crypto ETH as my two tokens because it makes it easier to intuit, though this generalizes to any pair of tokens (I like to think of prices in terms of dollars, not token A, but that's just me). The duration used to calculate the token changes implies the same LP hedging frequency. 24 hours is a pretty good frequency as hedge errors cancel out over a year via the law of large numbers, but anything between 6 hours and 1 week will generate similar numbers. If we can set ETHchange=0, USDchange will be near zero, and we will effectively eliminate IL.
An Extreme Base Case
One way to eliminate IL is to have a single LP who can trade for free while everyone else trades for a fee. Whenever the AMM price differs from the true price by less than the fee, only the LP can profit from arbitrage trading. A simple way to intuit this is to imagine if an AMM was created and not publicized, so it has no traders outside of the creator who assumes the role of LP and arbitrageur. With no other traders, he is trading with himself in a closed system. If his accounts are netted, he could both set the price on his contract efficiently and hedge his IL; nothing changes except the price. His net position in the tokens is static: ETHchange=0, IL=0.
It's helpful to think of traders as being two types: arbitrage and noise. Arbitrage traders are trying to make instant money off minor price discrepancies between exchanges; noise traders are like white noise, mean zero net demand that flows in like Brownian motion. A market price equilibrates supply and demand, so the volume that nets out is, by definition, noise. Noise traders are motivated by individual liquidity shocks, such as when a trader needs money to pay taxes, or the various random buy and sell signals generated by zero-alpha trading strategies.
If the AMM's base trading fee was 15 bps, and the LP could trade for free, the LP could turn loose an automated trading bot based on the Binance/CME/Coinbase price, trading whenever the mispricing exceeded 10 bps. Over time, the LP/arbitrager will be responsible for all the AMM's net price changes. With the AMM at the equilibrium price, immune to arbitrage by non-LP traders, the other trades will be white noise, net zero demand, by definition.
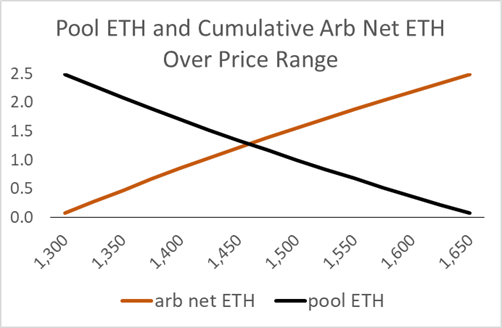
The figure below shows how the LP's ETH position for an AMM restricted range from $1300 to 1700 changes. The Pool ETH change implies traders are accumulating an offsetting amount; if the pool lost 2.5 ETH, traders gained 2.5 ETH. This net trader accumulation is arbitrage trading because it is not random, which is mean-zero over time. Gross trading will be greater due to noise trading, and in a healthy exchange, the noise traders will compensate the LP for his predictable IL over time.
If the monopolist zero-fee LP were the arbitrageur, at any price his net ETH position would be the same; the sum of those lines, his net position on the contract, would be horizontal. With a constant net ETH position, his impermanent loss would be zero. This works because, unlike traditional markets, the option seller is not reacting to prices but setting them. The latency inherent in any decentralized AMM implies the price setter does not need any alpha, just an API to the lower latency centralized exchanges.
The LP would still have exposure to this net ETH position, but this is simple to hedge off the AMM with futures, as it would not need frequent adjusting.
If we add a separate margin account on the contract that held the LP's trades (with himself), they will net to a constant, his initial token position. The monopolist LP's net position on the contract would be represented as in the table below (on average).
Single LP with Exclusive Arbitrage Trading Access
Thus, if the LP could trade for free, allowing him to dominate arbitrage, and he had a separate trading account on the contract, he could eliminate his IL without moving tokens on and off the blockchain or making other trades on different exchanges.
Multiple LPs
An AMM with only one LP would not work. An extensive set of LPs is needed to avoid centralization, which presents an attack surface for regulators and hackers; it is also needed to give the AMM unlimited scale. However, now we must consider LP competition. If we gave all the LPs free trading, a power law distribution of trading efficiency would invariably reveal a few dominant LPs monopolizing the arbitrage trading, shutting the slower LPs out and leaving them all exposed to IL as before.
Fortunately, the AMM provides a simple mechanism to allow all the LPs to arbitrage the price and hedge their positions simultaneously. This is because, on an AMM, the price is only changed by trades, so given a specific liquidity amount, a price change implies a specific change in ETH and vice versa. This makes it feasible to apply a rule using the LP's net ETH position on the contract to see if they qualify for the free discount.
Consider the following framework. Each LP gets a trading account in addition to their LP position. The key point is these accounts are netted, so like above, the LPs can retain a constant net position as the price moves significantly.
This can be adjusted to give them capital efficiency without changing the implications.[see footnote below] For my purpose in this post, this is irrelevant.
In the earlier example with one LP, his margin account's net change is calculated using the same liquidity as the pool because, with one LP, his liquidity is the pool's liquidity. This implied the LP's trades would always exactly offset his pool token changes. With many LPs, this is not so. A trade is against the entire pool, which is necessarily greater than any one LP. Thus, if LP(i) trades in a pool with many LPs, it will change LP(i)’s individual net position.
netETHchg(i) = (totLiq - liq(i))/totLiq *ETHtrade
As totLiq > liq(i), each trade changes the LP's net position, unlike when the monopolist LP trades with himself. For example, if an LP owns 10% of the liquidity, buying 1.0 token increases his margin position by 1.0 but decreases his pool position by only 0.1.
Assume LPs can only trade for free in the following conditions:
Buy for free only if
PoolEth(i) + MarginEth(i) - initEthDeposit(i) < + 0.01
Sell for free only if
PoolEth(i) + MarginEth(i) - initETHDeposit(i) > - 0.01
If we assume the LP hedged his initial ETH deposit off-chain, the rules basically say if an LP is net net long, he cannot buy for free; if the LP is net net short, he cannot sell for free [presuming she hedged elsewhere initially, her ‘net net' position is her net position minus her initial deposit, as we assume it is hedged].
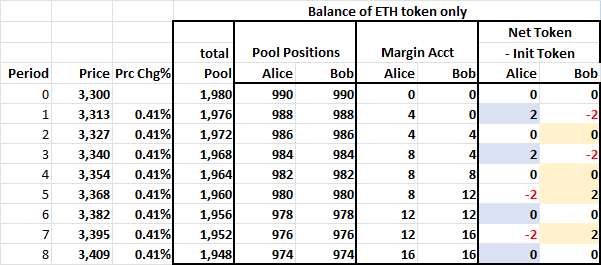
To see how this works, assume we have two LPs, Alice and Bob, with equal amounts of liquidity. Both Alice and Bob start with pool ETH positions of 990, and they have zero positions in their margin accounts. The trading fee is 0.5%, so all the price changes in this example are only profitable opportunities for Alice and Bob.
LP Pool, Margin, and Net ETH Balances
Assume the price initially rises by 0.41%, generating a arbitrage opportunity for the LPs. Alice wins the race and arbitrages this price discrepancy, setting the AMM price at its new equilibrium level of $3,313. She bought 4 ETH, and her pool position declined by 2 for a new ‘net net’ ETH position of +2. LP Bob just sees his pool position decline and has a new net net ETH position of -2; Bob is short, and Alice is long.
Alice cannot arb the AMM if the price rises again due to the rule preventing long LPs from buying at zero fee. If the price rises, Bob will win the arb race (by default), and LP’s Bob and Alice are each flat again. In the table above, Alice buys in the rows where she has a light blue box, and Bob buys in the rows where he has a light orange box. They can only buy when their net net position is flat or negative when prices are rising. This prevents Alice or Bob from dominating arbitrage.
If the price immediately went back down after Alice initially arbitraged the pool, only Alice could arbitrage the pool price. This is because in period 1, Alice is long, and Bob is short, so Bob cannot sell for free, while Alice can. When she does sell, she restores the initial net position for both herself and Bob. Alice’s extra trading is benign.
The LPs will experience net token position changes for single trades or small price movements. Over longer price movements, however, each individual LP's net token change would be insignificant, and assuming the LP hedged, their net net position would be insignificant.
There is no reason to pay arbs to set AMM prices, as the latency in decentralized blockchains implies arbitrage requires no special expertise, unlike the price discovery on the lowest latency exchanges. External arbitrageurs generate a deadweight loss for high-latency decentralized AMMs, so there is no trade-off with price efficiency.
A specialist with fast APIs and redundant arbitrage bot programs distributed in the cloud could manage a bot for a set of LPs. If the contract allowed LPs to whitelist another address that could do one thing on his account: trade for zero fee. The rule would prevent this arb vault manager from overtrading some accounts at the expense of others, as either it would single out one account for trades that cancel out, like in the case of Alice buying then selling above, or quickly find that her accounts that have traded first in one direction can no longer trade in that direction. One could cap trade size so the arb vault manager does not max out a trade on an LP to generate a profit for the other LPs. Competition among such specialists would allow passive LPs to get most of the benefit from arbitrage/hedging without creating and running their own arb bots.
It wouldn't work on coins not traded on major centralized exchanges because it presumes the true price is common knowledge. The next Shina Ibu will have to first trade on a conventional AMM. Yet, that's a minor amount of AMM volume.
Alternatives
As the equilibrium price is presumed to be on CEXes, and an equilibrium price implies net zero demand trading, one could use an oracle to update the AMM's last price to this price just as an LP arbitrage trade would. Over time, the LP net token changes would not be explicitly tied to price changes such that LP position values had negative convexity (i.e., linear in the square root of price). The main problem for oracle-based AMMs is centralization. This creates an attack surface for hackers. It also creates an attack surface for regulators, as the SEC knows where American Chainlink CEO Sergey Nazarov, for example, lives. Once they figure out how to do it—it took regulators several years to shut down InTrade—they will prevent his company from supporting anything that competes with regulated industries like finance and sports betting because regulation’s quid pro quo is protection from competition. Another problem is incentives, in that with more players with different actions, the state space complexity increases exponentially, so any solution will be more costly and less efficient. Arbitrageurs with more skin in the game would invest more time exploiting the oracle than the oracle would defending itself, especially as it requires a collective decision-making process and will be much slower to respond.
A decentralized limit order book (LOB) could avoid IL like an oracle-based AMM by allowing the LPs to move their resting limit orders costlessly to the latest CEX price, but there would be several problems. First, on-chain LOBs aspire to look and feel like the trading interfaces we are used to on centralized exchanges, so they emphasize low latency. Low latency leads to quasi, if not complete, centralization, an attack surface, and, more importantly, insiders who will get the equivalent of co-located server access. As third parties do not audit these ‘decentralized’ exchanges, the LOB leaders or a lower-level dev could sell undisclosed privileged access, and the costs would be virtually zero. It would take a lot of faith to presume they are immune to this subterfuge. Secondly, it would require many messages to cancel and replace resting limit orders. Unlike my mechanism, where one account rectifies the mispricing, on an LOB each LP account must be adjusted separately. On a CEX, these cancel-and-replace orders are costless, but if the blockchain is marginally decentralized, it will cost a few cents, and zero is a significant price point. Lastly, no one has presented a mechanism to incent a manager to oversee a set of LPs who wish to outsource their active management coherently. The LPs would still compete for favorable queue positioning, making it needlessly complicated and shutting out potential passive LPs.
The auction approach proposed by Maollemi et al. lets people bid to be the zero-fee trader. In that approach, the LPs would sell their right to fees to an arbitrageur who would get privileged zero-fee trading rights over some future period. The bidder pays a lump sum to the LPs, and the trading fees for that period go to the bid winner (meaning his trading fees return to him, so he trades for free). Assuming risk-neutrality and zero capital costs or other expenses, the arb would pay the expected arbitrage profit, which equals the expected LP convexity cost. They would also pay for the expected noise trader volume. Considering the arb bidder would be exposed to risk in that actual volatility and noise trader volume will be much lower than expected on occasion, he would pay considerably less than the expected value of the arbitrage opportunity and noise trading fees. The arb would have to hedge his trades on a different exchange, requiring extra collateral, and have to move tokens on and off the blockchain between those two exchanges (always losing one and gaining another). Lastly, frequent novel auctions can be manipulated, which means they will, especially at first.
Conclusion
The signature AMM is the ETH-USDC 5 bps pool on the Ethereum mainchain. Over the past 12 months, it has generated about $44MM in LP fee revenue and experienced $54MM in convexity costs. Yet even if LPs were, in aggregate, making a profit, the convexity cost is still significant and unnecessary. Given that the entire Uniswap AMM market is 4x the above pool, and there are other AMM protocols, that's several hundred million dollars a year wasted annually. The good news is this can be eliminated, propelling AMMs out of their doldrums and securing a long-term solution to an essential blockchain mechanism: swapping coins.
Most crypto people do not intuitively understand an LP's convexity costs, but they are not some new speculative theory (e.g., hedge fund sniping). Gamma, convexity costs, and theta decay have been analyzed empirically and theoretically for the past 50 years. They are the unavoidable consequence of convex payouts based on an exogenous underlying stochastic price. Constant product AMMs that link trade amounts to price changes, combined with the latency, allow the derivative owner (LP) to both hedge and set the underlying price simultaneously.
I haven't met anyone who understands this because they would be excited if they did. It's not often you find ways of saving hundreds of millions of dollars a year. My friends in academia or tradFi don't have much interest, let alone knowledge, of AMMs. My acquaintances in crypto, even those actively building AMMs, don't understand convexity beyond the technical definition, so they do not think it is a big deal. Fear of convexity costs is the beginning of AMM wisdom.
I wrote my dissertation in 1994 on low-vol stocks, noting they generated abnormal returns because they generate a slight premium to the market at 30% less risk (see here for a history of low-vol investing). I took a job as a bank risk manager but was busy pitching the idea to various asset managers, including several at the major investment banks. They didn't reject what I was saying but were always eager to know if well-known people or institutions in this field were on board. They weren't, and no one thought a fund offering virtually the same return as the SP500, regardless of risk, was compelling. I was out by the time low-vol investing started to grow. The responses I get from crypto people to this idea are similar.
It's not an abstract argument, just MBA-level finance. My best hope for this approach is that in a few years, LLMs will pick it up as they scrape the web for data, and via pure logic, over a couple of years, ChatGPT6 will use it as an answer for 'How do I remove impermanent loss?' There is pleasure in just being right about something important.
footnote

In a levered AMM, the initial pool amounts are multiples of the initial deposit. This implies the LP starts with debits in his margin account for both tokens. The process works as follows:
Take an initial ETH deposit, ETH0. Given the initial price, p0, and assuming a leverage of 20x, apply the following liquidity to that LP
liquidity = 20*sqrt(p0)*ETH0
Given that liquidity, the initial USD deposit, also levered 20 times, is calculated:
Initial USD deposit = liquidity*sqrt(p0)/20
The objective of monitoring the LP’s net position for free trading is the same as above. Here, the initial margin account is negative, and the LP is susceptible to insolvency. However, a more pressing concern is whether the LP will be insolvent in one of the tokens, even though their total position value is positive. A pool where all the LPs are solvent, but the LPs have zero of one of the tokens would prevent purchases of that token. The solution is to allow liquidation based also on the minimum net position for the LP in the two tokens.
If the LP actively hedges its position, its net position will be constant in both tokens, so LPs would only be subject to liquidation if they exposed themselves to IL out of negligence.


No comments:
Post a Comment